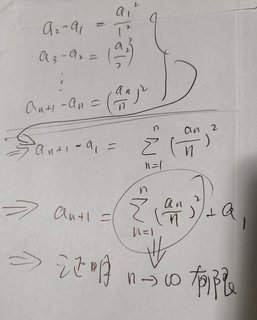阿里巴巴决赛试题
版主： Softfist
-
Edwinjiangjjjj（Edwinjiang）
- 见习点评
- 帖子互动： 14
- 帖子： 1797
- 注册时间： 2022年 8月 3日 07:17
#5 Re: 阿里巴巴决赛试题
我不去想是否能够成功
既然选择了远方
便只顾风雨兼程
我不去想身后会不会袭来寒风冷雨
既然目标是地平线
留给世界的只能是背影
我不去想未来是平坦还是泥泞
只要热爱生命
一切，都在意料之中
既然选择了远方
便只顾风雨兼程
我不去想身后会不会袭来寒风冷雨
既然目标是地平线
留给世界的只能是背影
我不去想未来是平坦还是泥泞
只要热爱生命
一切，都在意料之中
x2
大海当尿盆
地球作屎坑
我菊一开口
清气满乾坤
ziyan
-
bluebottle
- 著名点评
- 帖子互动： 90
- 帖子： 4265
- 注册时间： 2022年 12月 18日 19:06
-
bluebottle
- 著名点评
- 帖子互动： 90
- 帖子： 4265
- 注册时间： 2022年 12月 18日 19:06
-
greenspring
- 见习点评
- 帖子互动： 59
- 帖子： 1349
- 注册时间： 2022年 7月 21日 23:27
#18 Re: 阿里巴巴决赛试题
0<=a1<1
a_(n+1)= a_n + (a_n)^2/n^2
a1<1
a2= a1 + a1^2= a1(1+a1) < 2
a3= a2+ a2^2/4 = a2 (1+ a2/4) < 3
…
We can have a_n<n
a_(n+1)/a_n= 1 + a_n/n^2 < 1+ n/n^2 = 1+1/n
a_(n+1)< (1+1/n) a_n
Since Lim (1+1/n)^n = e
Then Lim(a_n) = L is bounded.
a_(n+1)= a_n + (a_n)^2/n^2
a1<1
a2= a1 + a1^2= a1(1+a1) < 2
a3= a2+ a2^2/4 = a2 (1+ a2/4) < 3
…
We can have a_n<n
a_(n+1)/a_n= 1 + a_n/n^2 < 1+ n/n^2 = 1+1/n
a_(n+1)< (1+1/n) a_n
Since Lim (1+1/n)^n = e
Then Lim(a_n) = L is bounded.
x1
#19 Re: 阿里巴巴决赛试题
17岁中专服装姜神能想到这个，非常了不起了greenspring 写了： 2024年 6月 23日 13:17 0<=a1<1
a_(n+1)= a_n + (a_n)^2/n^2
a1<1
a2= a1 + a1^2= a1(1+a1) < 2
a3= a2+ a2^2/4 = a2 (1+ a2/4) < 3
…
We can have a_n<n
a_(n+1)/a_n= 1 + a_n/n^2 < 1+ n/n^2 = 1+1/n
a_(n+1)< (1+1/n) a_n
Since Lim (1+1/n)^n = e
Then Lim(a_n) = L is bounded.
肘子急得连夜会把阿里祖坟刨了
大海当尿盆
地球作屎坑
我菊一开口
清气满乾坤
ziyan
-
greenspring
- 见习点评
- 帖子互动： 59
- 帖子： 1349
- 注册时间： 2022年 7月 21日 23:27
