分页: 2 / 3
#22 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 28日 16:03
由 lonelyarcher
作为一个马工,看都看不懂
#23 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 28日 16:42
由 TheMatrix
唯一能看懂的就是分析类第四题。

#24 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 28日 17:14
由 longtian
想了一下,看看可不可以这么做
1.a1=0,显然都是0,OK
2. 0< a1<1的时候,数列是单调递增,所以a(n)< a(n+1),
a(n+1)-a(n)= a(n)^2/n^2 < a(n)*a(n+1)/n^2
So 1/a(n) - 1/a(n+1) < 1/n^2 < 1/(n*n(-1)) , we can get
1/a(1) - 1/a(n) < 1-1/(n-1) ,thus a(n) < 1 / (1/a(1) - (1-1/n)) <1/(1/a(1)+1)
TheMatrix 写了: 2024年 6月 24日 22:05
这个我有思路了。我觉得我应该是能写出来的。但是一个人玩没啥意思。我先不写。
#25 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 28日 17:22
由 TheMatrix
longtian 写了: 2024年 6月 28日 17:14
想了一下,看看可不可以这么做
1.a1=0,显然都是0,OK
2. 0< a1<1的时候,数列是单调递增,所以a(n)< a(n+1),
a(n+1)-a(n)= a(n)^2/n^2 < a(n)*a(n+1)/n^2
So 1/a(n) - 1/a(n+1) < 1/n^2 < 1/(n*n(-1)) , we can get
1/a(1) - 1/a(n) < 1-1/(n-1) ,thus a(n) < 1 / (1/a(1) - (1-1/n)) <1/(1/a(1)+1)
你最后这个结果是不对的:
a(n) < 1/(1/a(1)+1)
比如a
1= 0.9。按你这个结果,a
n < 1/(1/0.9 +1) ≈ 0.5。
这显然是不对的。
#26 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 28日 17:25
由 longtian
我也发现了,好像需要分情况讨论a(1)的范围,还有我那个放缩太粗糙,我再想一下
TheMatrix 写了: 2024年 6月 28日 17:22
你最后这个结果是不对的:
a(n) < 1/(1/a(1)+1)
比如a
1= 0.9。按你这个结果,a
n < 1/(1/0.9 +1) ≈ 0.5。
这显然是不对的。
#27 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 28日 17:33
由 FoxMe
p=5的时候就有。这样乘开来不大可行,应该是个简单式子
TheMatrix 写了: 2024年 6月 28日 15:55
p=7的时候,方程写出来是:
X**3
- 2*X**2*Y*cos(2*pi/7)
+ 2*X**2*Y*cos(3*pi/7)
+ 2*X**2*Y*cos(pi/7)
- 4*X*Y**2*cos(pi/7)*cos(2*pi/7)
- 4*X*Y**2*cos(2*pi/7)*cos(3*pi/7)
+ 4*X*Y**2*cos(pi/7)*cos(3*pi/7)
- 8*Y**3*cos(pi/7)*cos(2*pi/7)*cos(3*pi/7)
= 49
这要有整数解就奇怪了。

#28 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 28日 17:43
由 TheMatrix
FoxMe 写了: 2024年 6月 28日 17:33
p=5的时候就有。这样乘开来不大可行,应该是个简单式子
嗯。p=5的时候左边乘积等于:
X**2 + X*Y - Y**2
系数刚好都是整数。
#29 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 28日 17:48
由 FoxMe
左边 = Norm(X - 2cos(2*pi/p)*Y),从p的ideal分解去想,是一条思路。
还有一条思路是用Eisenstein准则,证明prod(X - 2cos(2*pi*k/p)*Y) - p^2不可约。先要把prod(X - 2cos(2*pi*k/p)*Y)化简为整系数多项式。
#30 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 28日 17:59
由 TheMatrix
FoxMe 写了: 2024年 6月 28日 17:48
左边 = Norm(X - 2cos(2*pi/p)*Y),从p的ideal分解去想,是一条思路。
还有一条思路是用Eisenstein准则,证明prod(X - 2cos(2*pi*k/p)*Y) - p^2不可约。先要把prod(X - 2cos(2*pi*k/p)*Y)化简为整系数多项式。
嗯。你这个思路好。马上就高大上起来。

Norm是数域的norm吧?但是(X - 2cos(2*pi/p)*Y)不是数域中的元素。
prod(X - 2cos(2*pi*k/p)*Y)也不可能是整系数吧?
#31 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 28日 18:02
由 FoxMe
Norm是数域的norm,(X - 2cos(2*pi/p)*Y)是数域中的元素(p阶分圆域Q(exp(2*pi*i/p))或它的实子域Q(2cos(2*pi/p))。我猜prod(X - 2cos(2*pi*k/p)*Y)是整系数。
还可以这样试:因为p = prod(2 - 2cos(2*pi*k/p)),所以要证明
prod(X - 2cos(2*pi*k/p)*Y) = prod(2 - 2cos(2*pi*k/p)) * prod(2 - 2cos(2*pi*k/p))
如果没有平方,有解X=2, Y=1。但是现在有平方。
如果证明上式等同于证明下式(
差这一步)
X - 2cos(2*pi/p)*Y = (2 - 2cos(2*pi/p)) * (2 - 2cos(2*pi/p))
无解,那就证完了(p>5时显然无解)。
TheMatrix 写了: 2024年 6月 28日 17:59
嗯。你这个思路好。马上就高大上起来。

Norm是数域的norm吧?但是(X - 2cos(2*pi/p)*Y)不是数域中的元素。
prod(X - 2cos(2*pi*k/p)*Y)也不可能是整系数吧?
#32 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 28日 21:35
由 TheMatrix
FoxMe 写了: 2024年 6月 28日 18:02
Norm是数域的norm,(X - 2cos(2*pi/p)*Y)是数域中的元素(p阶分圆域Q(exp(2*pi*i/p))或它的实子域Q(2cos(2*pi/p))。我猜prod(X - 2cos(2*pi*k/p)*Y)是整系数。
还可以这样试:因为p = prod(2 - 2cos(2*pi*k/p)),所以要证明
prod(X - 2cos(2*pi*k/p)*Y) = prod(2 - 2cos(2*pi*k/p)) * prod(2 - 2cos(2*pi*k/p))
如果没有平方,有解X=2, Y=1。但是现在有平方。
如果证明上式等同于证明下式(
差这一步)
X - 2cos(2*pi/p)*Y = (2 - 2cos(2*pi/p)) * (2 - 2cos(2*pi/p))
无解,那就证完了(p>5时显然无解)。
嗯。这个问题用分圆域证明确实很relevant。我不太熟分圆域,所以没往那边想。
我把(X - 2cos(2*pi*k/p)*Y)看成是C[X,Y] polynomial的元素了,应该把它看成是X,Y整数系数,所以是分圆域里的元素。
但是你说p = prod(2 - 2cos(2*pi*k/p))。这个成立吗?我试了一下p=7,好像不对。
#33 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 28日 22:17
由 TheMatrix
TheMatrix 写了: 2024年 6月 28日 14:55
如果把x/(1+cx)看成是c-parameter family of curves,那么这个曲线族是充满三角区域(y<x)的。也就是每一个点(n,a
n)都有一个曲线恰好通过它。每一个(n,a
n)对应的c都不同,但是不应该相差太大。这应该有一个定理保证。
我说的这个定理应该这么表述:
数列的递推定义
u
n+1-u
n=f(u
n,n)
与相应的微分方程
u'=f(u,x)
在第一项相等的情况下,u
n与u(x)在 n --> ∞ 和 x --> ∞下有相同的收敛性 - 都收敛或者都不收敛。收敛的话,相差一个常数。
下图是a
1=0.9,红色曲线是数列,蓝色曲线是微分方程得出的曲线:
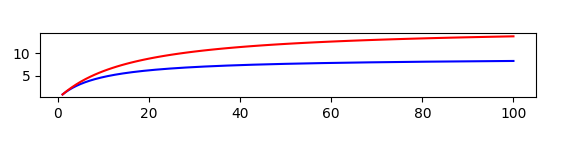
#34 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 29日 12:56
由 TheMatrix
TheMatrix 写了: 2024年 6月 28日 22:17
我说的这个定理应该这么表述:
数列的递推定义
u
n+1-u
n=f(u
n,n)
与相应的微分方程
u'=f(u,x)
在第一项相等的情况下,u
n与u(x)在 n --> ∞ 和 x --> ∞下有相同的收敛性 - 都收敛或者都不收敛。收敛的话,相差一个常数。
下图是a
1=0.9,红色曲线是数列,蓝色曲线是微分方程得出的曲线:

数列和相应微分方程曲线的关系,非常类似于
Σ 1/n 和 ∫ 1/x dx
的关系。说明的方法也应该非常类似。但是不知道怎么说明。
#35 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 29日 13:20
由 TheMatrix
TheMatrix 写了: 2024年 6月 29日 12:56
数列和相应微分方程曲线的关系,非常类似于
Σ 1/n 和 ∫ 1/x dx
的关系。说明的方法也应该非常类似。但是不知道怎么说明。
调整参数c,相当于调整a
1点。下面三根蓝色的曲线,从下到上分别是:
a
1=0.9
a
1=0.93
a
1=0.95
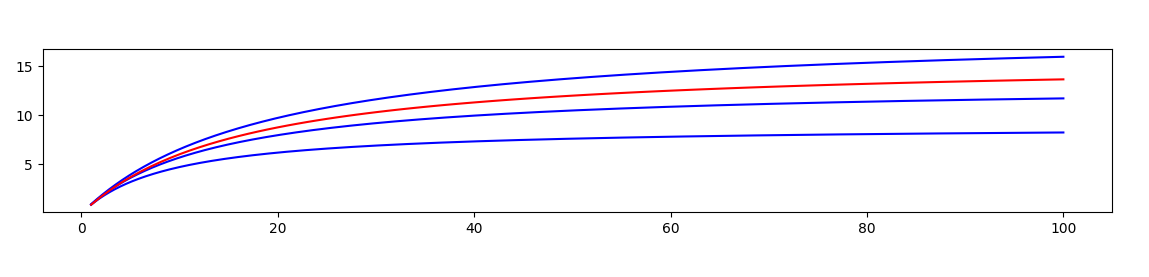
放大之后可以看到
a
1=0.9的曲线完全在数列(红色曲线)的下方,
a
1=0.95的曲线完全在数列的上方,
而a
1=0.93的曲线和数列曲线相交,
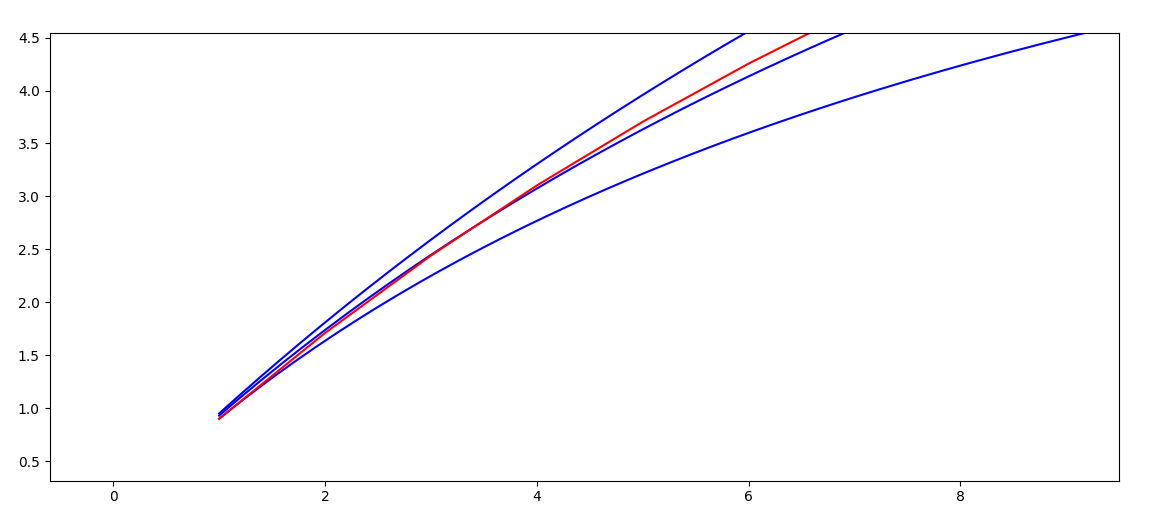
所以接下来应该证明,可以找到一条曲线(参数c),使得该曲线完全在数列曲线的上方。
#36 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 29日 13:46
由 TheMatrix
TheMatrix 写了: 2024年 6月 29日 13:20
调整参数c,相当于调整a
1点。下面三根蓝色的曲线,从下到上分别是:
c=0.9
c=0.93
c=0.95

放大之后可以看到
c=0.9的曲线完全在数列(红色曲线)的下方,
c=0.95的曲线完全在数列的上方,
而c=0.93的曲线和数列曲线相交,

所以接下来应该证明,可以找到一条曲线(参数c),使得该曲线完全在数列曲线的上方。
调整参数c和调整a(1)是一样的,因为a(x)=x/(1+cx),a(1)=1/(1+c),c=(1/a(1))-1。
很显然如果某a(1) ∈ (0,1) 使得蓝色曲线完全在红色曲线上方,那么取大一点的a(1)更加有蓝色曲线在红色曲线上方。所以使蓝色曲线完全在红色曲线上方的a(1)的集合,有下界。问题:这个集合有没有下确界?(等同于问相应的c集合有没有上确界)。也就是问集合在下界方向上是开集还是闭集。
#37 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 29日 14:15
由 TheMatrix
TheMatrix 写了: 2024年 6月 28日 15:55
p=7的时候,方程写出来是:
X**3
- 2*X**2*Y*cos(2*pi/7)
+ 2*X**2*Y*cos(3*pi/7)
+ 2*X**2*Y*cos(pi/7)
- 4*X*Y**2*cos(pi/7)*cos(2*pi/7)
- 4*X*Y**2*cos(2*pi/7)*cos(3*pi/7)
+ 4*X*Y**2*cos(pi/7)*cos(3*pi/7)
- 8*Y**3*cos(pi/7)*cos(2*pi/7)*cos(3*pi/7)
= 49
这要有整数解就奇怪了。

p=7的分圆域是degree 6 over Q。把cos(k*pi/7)乘积部分按照分圆域基写出来。按分量collect系数,得到6个方程,复数的。按实部和虚部分,得到12个含X和Y系数的方程。证明这12个方程的方程组没有整数解。思路就是这么个思路。

#38 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 29日 18:00
由 FoxMe
你的思路很好,其实没那么复杂。要在分圆域的maximal totally real subfield Q(cos(pi/7))上考虑,这个子域的阶为3,所以只有3个实数方程。
因为这个子域的基为{1, cos(pi/7), cos(2pi/7)},所以可把方程写为
X**3 + Y*(...)
+ Y*(...)*cos(pi/7)
+ Y*(...)*cos(2*pi/7)
= 49
注意到Y必然=0,所以推出X**3 = 49,显然无解。
一般情况下,也能推出Y=0,X**((p-1)/2) = p**2,p>5时无整数解。这里的关键是其它项都有Y。
以上证明有没有错误?
TheMatrix 写了: 2024年 6月 29日 14:15
p=7的分圆域是degree 6 over Q。把cos(k*pi/7)乘积部分按照分圆域基写出来。按分量collect系数,得到6个方程,复数的。按实部和虚部分,得到12个含X和Y系数的方程。证明这12个方程的方程组没有整数解。思路就是这么个思路。

#40 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 29日 18:30
由 FoxMe
好了,下面有空再去做数论代数的第一题,以前讨论表示论的时候有些触及,应该能做。
#41 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 29日 21:53
由 TheMatrix
FoxMe 写了: 2024年 6月 29日 18:00
你的思路很好,其实没那么复杂。要在分圆域的maximal totally real subfield Q(cos(pi/7))上考虑,这个子域的阶为3,所以只有3个实数方程。
因为这个子域的基为{1, cos(pi/7), cos(2pi/7)},所以可把方程写为
X**3 + Y*(...)
+ Y*(...)*cos(pi/7)
+ Y*(...)*cos(2*pi/7)
= 49
注意到Y必然=0,所以推出X**3 = 49,显然无解。
一般情况下,也能推出Y=0,X**((p-1)/2) = p**2,p>5时无整数解。这里的关键是其它项都有Y。
以上证明有没有错误?
这里可能有一个问题。比如这一项:
Y*(...)*cos(pi/7)
cos(pi/7)系数等于0,不一定Y=0,也可以(...)=0,因为括号里面是X,Y的一个多项式。
#42 Re: (转载)阿里巴巴决赛试题
发表于 : 2024年 6月 30日 10:45
由 FoxMe
这是个漏洞,我考虑过,觉得如果(...)=0,那么那一项就没了,但是忽略了X**3 + Y*(...)中的(...)。但是只要找出任一cos项(...)不等于0就够了。
也就是说,对于p=7这个例子,
X**3 + Y*(...)
+ Y*(...)*cos(pi/7)
+ Y*(...)*cos(2*pi/7)
= 49
我的漏洞只有当Y*(...)*cos(pi/7),Y*(...)*cos(2*pi/7)中的(...)都=0, 并且X**3 + Y*(...)中的(...)不为0的时候才出现。
TheMatrix 写了: 2024年 6月 29日 21:53
这里可能有一个问题。比如这一项:
Y*(...)*cos(pi/7)
cos(pi/7)系数等于0,不一定Y=0,也可以(...)=0,因为括号里面是X,Y的一个多项式。





