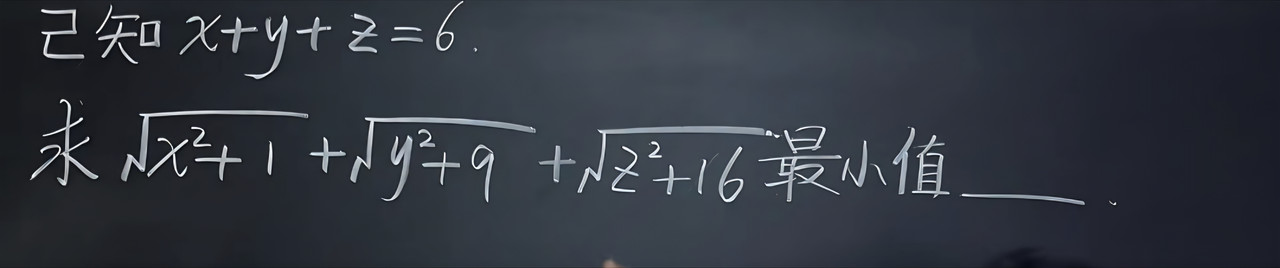分页: 2 / 2
#21 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 6月 26日 23:27
由 juderiverman
ILoveBainiu 写了: 2025年 6月 26日 23:14
The expression to minimize is sqrt(x² + 1²) + sqrt(y² + 3²) + sqrt(z² + 4²).
Each term in the sum can be interpreted as the length of the hypotenuse of a right triangle, or as the distance between two points in a 2D plane.
Let's visualize this as the length of a path made of three segments:
A segment with a horizontal displacement of x and a vertical displacement of 1. Its length is sqrt(x² + 1²).
A segment with a horizontal displacement of y and a vertical displacement of 3. Its length is sqrt(y² + 3²).
A segment with a horizontal displacement of z and a vertical displacement of 4. Its length is sqrt(z² + 4²).
The total length of this path is the sum we want to minimize. The path starts at an origin point, say (0,0), and ends at the point whose coordinates are the sum of the displacements.
The total horizontal displacement is x + y + z.
The total vertical displacement is 1 + 3 + 4 = 8.
We are given the constraint that x + y + z = 6. Therefore, the path connects the starting point (0, 0) to the fixed endpoint (6, 8).
The sum of the lengths of the path segments is minimized when the path is a straight line. The minimum value of the expression is therefore the straight-line distance between the point (0, 0) and the point (6, 8).
We can calculate this distance using the distance formula:
Distance = sqrt((6 - 0)² + (8 - 0)²)
Distance = sqrt(6² + 8²)
Distance = sqrt(36 + 64)
Distance = sqrt(100)
Distance = 10
Thus, the smallest possible value of the expression is 10.
看看gemini多牛逼
这个太厉害了
#22 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 6月 26日 23:31
由 shuiya
柯西不等式 直接套
#23 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 6月 26日 23:34
由 yuzhou
sqrt(x^2+1) + sqrt(y^2+9) + sqrt(z^2+16) >=sqrt(2x) + sqrt(6y)+sqrt(8z)
有题目对称性得到
3(sqrt(x^2+1) + sqrt(y^2+9) + sqrt(z^2+16) ) >= (sqrt(2)+sqrt(6)+sqrt(8)) (sqrt(x) + sqrt(y)+sqrt(z))
(sqrt(x) + sqrt(y)+sqrt(z))^2 =x+y+z + sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(y) sqrt(z) =6+ sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(x) sqrt(z)
由柯西不等式 (x+y+x)^2>=(sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(x) sqrt(z))^2
sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(x) sqrt(z)<=6
3倍的最小值 是(sqrt(2)+sqrt(6)+sqrt(8))*sqrt(12)
最小值是 (2sqrt(6) +6sqrt(2)+8sqrt(3))/3
#24 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 6月 26日 23:52
由 juderiverman
yuzhou 写了: 2025年 6月 26日 23:34
sqrt(x^2+1) + sqrt(y^2+9) + sqrt(z^2+16) >=sqrt(2x) + sqrt(6y)+sqrt(8z)
如果这样的话,X应该最大,Y其次,Z最小;
假定X,Y,Z都是正整数,那应该是3,2,1……
sqrt(10)+sqrt(13)+sqrt(17)=10.891
这组值不如1,2,3……
sqrt(2)+sqrt(13)+sqrt(25)=10.0198
类似长方形到正方形的变化,应该是Z>Y>X,因为16>9>1。
#25 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 6月 27日 00:23
由 mzliew
这样不行的,不等式右边只是给了左边的一个下界,但不一定是下确界。比如说你可以说三个平方根之和肯定大于等于0, 但0不一定是最小值。下确界才是最小值。你列出来的那个值,算出来是9.08,确实比10小,但永远都到不了这么小。
yuzhou 写了: 2025年 6月 26日 23:34
sqrt(x^2+1) + sqrt(y^2+9) + sqrt(z^2+16) >=sqrt(2x) + sqrt(6y)+sqrt(8z)
有题目对称性得到
3(sqrt(x^2+1) + sqrt(y^2+9) + sqrt(z^2+16) ) >= (sqrt(2)+sqrt(6)+sqrt(8)) (sqrt(x) + sqrt(y)+sqrt(z))
(sqrt(x) + sqrt(y)+sqrt(z))^2 =x+y+z + sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(y) sqrt(z) =6+ sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(x) sqrt(z)
由柯西不等式 (x+y+x)^2>=(sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(x) sqrt(z))^2
sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(x) sqrt(z)<=6
3倍的最小值 是(sqrt(2)+sqrt(6)+sqrt(8))*(sqrt(12))/3
最小值是 (2sqrt(6) +6sqrt(2)+8sqrt(3))/3
#26 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 6月 27日 00:41
由 OzarkAna
真闲的蛋疼
#27 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 6月 27日 00:52
由 Yesterday
ILoveBainiu 写了: 2025年 6月 26日 23:14
The expression to minimize is sqrt(x² + 1²) + sqrt(y² + 3²) + sqrt(z² + 4²).
Each term in the sum can be interpreted as the length of the hypotenuse of a right triangle, or as the distance between two points in a 2D plane.
Let's visualize this as the length of a path made of three segments:
A segment with a horizontal displacement of x and a vertical displacement of 1. Its length is sqrt(x² + 1²).
A segment with a horizontal displacement of y and a vertical displacement of 3. Its length is sqrt(y² + 3²).
A segment with a horizontal displacement of z and a vertical displacement of 4. Its length is sqrt(z² + 4²).
The total length of this path is the sum we want to minimize. The path starts at an origin point, say (0,0), and ends at the point whose coordinates are the sum of the displacements.
The total horizontal displacement is x + y + z.
The total vertical displacement is 1 + 3 + 4 = 8.
We are given the constraint that x + y + z = 6. Therefore, the path connects the starting point (0, 0) to the fixed endpoint (6, 8).
The sum of the lengths of the path segments is minimized when the path is a straight line. The minimum value of the expression is therefore the straight-line distance between the point (0, 0) and the point (6, 8).
We can calculate this distance using the distance formula:
Distance = sqrt((6 - 0)² + (8 - 0)²)
Distance = sqrt(6² + 8²)
Distance = sqrt(36 + 64)
Distance = sqrt(100)
Distance = 10
Thus, the smallest possible value of the expression is 10.
看看gemini多牛逼
看来你得到白牛指导了。用几何解决代数问题是另一个维度
#28 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 7月 1日 03:39
由 ILoveBainiu
Yesterday 写了: 2025年 6月 27日 00:52
看来你得到白牛指导了。用几何解决代数问题是另一个维度
菌斑僵菌很多看不懂拉格朗日,就不贴了
#29 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 7月 1日 03:43
由 bam
这不虾扯蛋吗,但凡不是文科生谁不懂拉格朗日乘数法啊
#30 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 7月 1日 03:54
由 ILoveBainiu
bam 写了: 2025年 7月 1日 03:43
这不虾扯蛋吗,但凡不是文科生谁不懂拉格朗日乘数法啊
千老未必会
#31 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 7月 1日 03:55
由 bam
#32 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 7月 1日 05:07
由 LiuQiangDong
俩子空间相切吧
gemini的解法是做题家解法
投机取巧
好处是速度快
容易拿分
坏处是不普世
限制思维扩展
#33 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 7月 1日 06:30
由 ziganwu
把做题的时间用来多操逼也不会落得今天的下场
#34 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 7月 1日 07:27
由 OPQ
A nice problem with nice solutions.
#35 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 7月 1日 07:39
由 SidRat
数形结合,答案是10啦!

#36 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 7月 1日 08:08
由 SidRat
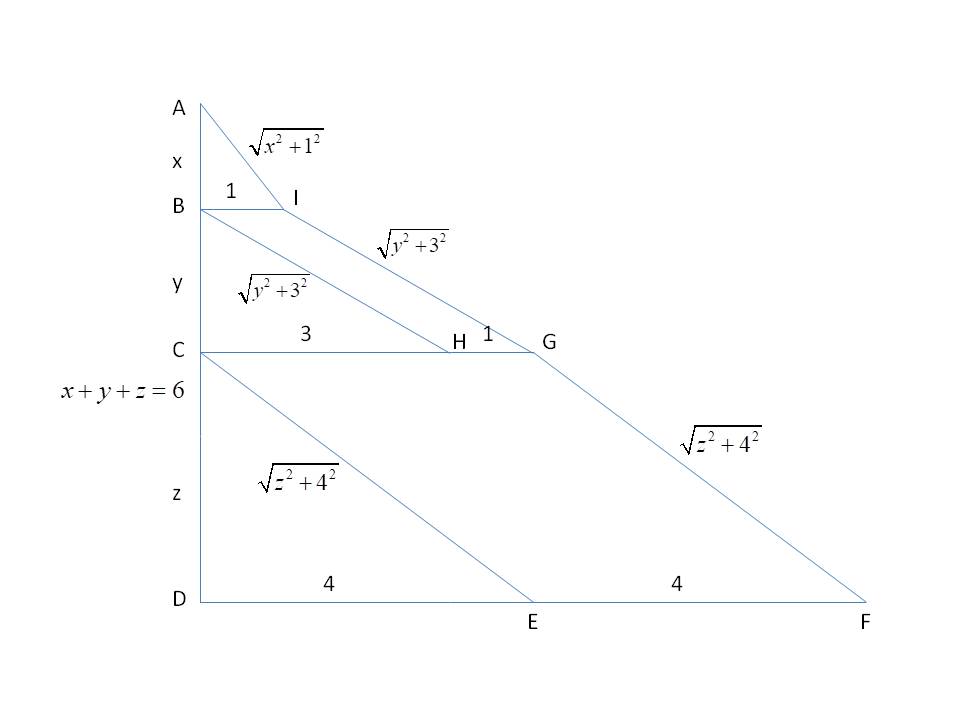
数形结合,答案是10啦!

如下图所示,要使3项之和最小,那么就需要A、I、G、F四点共线,此时AF = sqrt(6^2 + (4+4)^2) = 10。
#37 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 7月 1日 08:18
由 大巨魔
SidRat 写了: 2025年 7月 1日 08:08
数形结合,答案是10啦!

如下图所示,要使3项之和最小,那么就需要A、I、G、F四点共线,此时AF = sqrt(6^2 + (4+4)^2) = 10。

你这个图再优化一下就是标准答案了
#38 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 7月 1日 09:21
由 lpz9678
SidRat 写了: 2025年 7月 1日 08:08
数形结合,答案是10啦!

如下图所示,要使3项之和最小,那么就需要A、I、G、F四点共线,此时AF = sqrt(6^2 + (4+4)^2) = 10。

没错。基本原理是,要让三个变量之和最小的话,需要三个变量等比例,也就是三个小直角三角形相似,而且还都跟大直角三角形相似。根据相似性,口算都可以得出 xyz的值,以及斜边和的值
#39 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 7月 1日 09:44
由 lpz9678
LiuQiangDong 写了: 2025年 7月 1日 05:07
俩子空间相切吧
gemini的解法是做题家解法
投机取巧
好处是速度快
容易拿分
坏处是不普世
限制思维扩展
什么思维扩展,扩展了还是格局太小。你看不到题目顶(底)层的逻辑。要让几个受线性约束的变量之和最小,这几个变量互相要成比例。这就是这个问题最底层的逻辑,根据三角形的相似性,口算都可以得出xyz的值
#40 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
发表于 : 2025年 7月 1日 10:03
由 马大帅
无所谓
全世界还活着的赤手空拳把老婆打死的人我看也不超过五个
那又怎样