annorying0 写了： 2025年 11月 2日 22:39我来，出错当积人品。
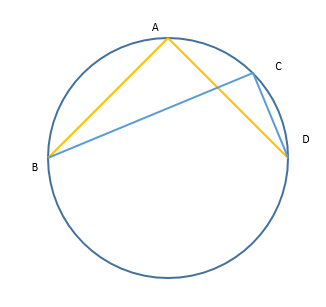
以A 为顶点画等腰三角型，其余2点为B,D AB=AD
然后用一个圆规以 A为圆点，BD长为半径画一段弧，弧上点为C 有无数多个点。所以我结论是三角形可以不全等
(我将写错的等边改回了等腰,已经忘记那叫等腰了)
no, angle BDC and DBC only add up to the same, not equal to each other
verdelite 写了： 2025年 11月 2日 22:36不证明，就画个角BAD，从角A引出一个角内部的射线，如果是角平分线肯定成立，如果不是角平分线，第四个点C从射线上的A点变化到无穷，观察两个对角啥时相等。也就两个地方相等：1，C=A; 2，BCD在一条直线上。
跟着感觉走？对直觉派只能羡慕，无话可说。
从等腰三角型(AB=AD)顶点 A 画一条垂直于BD的直线, C点 一定在这直线上. 因为 角 B= 角 D
(要证明,不过一画就确定)
所以2个三角形相同
三角形中其它两个角相等了， 剩下一角一定也相等啊
看来你们初二的平面几何或者学的不如我，或者忘记了。两边和一个角相等的三角形不一定相等，要相等必须两边夹，这在初二就是定论了。
annorying0 写了： 2025年 11月 2日 23:36从等腰三角型(AB=AD)顶点 A 画一条垂直于BD的直线, C点 一定在这直线上. 因为 角 B= 角 D
(要证明,不过一画就确定)所以2个三角形相同
其实也是一个证明的思路，只是没有用严格的数学公式写下来。
huangchong 写了： 2025年 11月 2日 23:32no, angle BDC and DBC only add up to the same, not equal to each other
我之前没有看明白题目.所以错了.
任意四边形，画就带偏了，自己脑补。
简单证明：以A为圆心，AB为半径画圆，B，D必在圆上。若C在圆外，角B和角D在0-180度之间变化，但都只有唯一值，故两三角形全等。若C在圆内，角B,D分别从0增大再减小到0，有两个角度值可以相同，所以可有不等三角形。
你这不对，“对角线AC”
如果不考虑这种情况，那题目就是永远全等，因为很容易得知角BDC和角DBC一样大，包括C角往里凹陷的情况。也就是说CBD也是等腰三角形。
三边都相等不就是全等么？
hereyouare 写了： 2025年 11月 2日 18:30任意一个4边形，ABCD，对角线AC截成了上下两个三角形，同边AC的对角B和D相等，AB和AD两边也相等。上下两个三角形肯定全等吗？
去国多年，没想到国内的初中教育能出这个大的漏勺。deepseek，chatgpt第一遍也全错。
这是初中平面几何题，限于尺规证明，别提sin，cos。。
huangchong 写了： 2025年 11月 2日 23:54如果不考虑这种情况，那题目就是永远全等，因为很容易得知角BDC和角DBC一样大，包括C角往里凹陷的情况。也就是说CBD也是等腰三角形。
还有这种考虑。。。没有想到 
huangchong 写了： 2025年 11月 2日 23:54如果不考虑这种情况，那题目就是永远全等，因为很容易得知角BDC和角DBC一样大，包括C角往里凹陷的情况。也就是说CBD也是等腰三角形。
斌狗。
只除了bcd是共线的情况，但那个退化成三角形，不再是四边形，理应排除。
总结一下，全国教育云平台机械的以边边角不一定全等做了否定回答，甚至也不找个反例，其实找找就会发现找不出反例。几个ai也是在我一再逼问反例的情况下大都纠正了错误。边边角不全等的情况只有在bcd共边时才会发生，即abd是一个等腰三角形，而c是bd边上除了中点的任意一点，这样，上下两个三角形满足边边角但不全等，但是这已不符合四边形的定义。原题实际上画了个凸四边形，如果不全等，则ac必然不是a的角平分线，肯定靠近上或下，在ab和ad相等，角b和角d相等的情况下，bc和dc直觉就不该能重合在c点。好奇全国云平台推出几年了，没人发现吗？
返利很好找
B和D在以A为圆心的圆上
C假设在圆内
B从AC延长线沿圆周滑到CA延长线
B角从0增加又回到0
中间必定有两个同角度的点
一个算B一个算D
再把其中一个镜像翻转
SSA不能用来证明是全等三角形的原因是，正弦定理求解可能会有两个角度。要么得到相等的角，要么得到补角。这题如果角ACB和角ACD是补角的话，就会造成BCD共线，从而ABCD不再是四边形。所以只能是第一种情况，那么上下两个三角形就必定是全等的。
LiuQiangDong 写了： 2025年 11月 3日 01:35返利很好找
B和D在以A为圆心的圆上
C假设在圆内
B从AC延长线沿圆周滑到CA延长线
B角从0增加又回到0
中间必定有两个同角度的点
一个算B一个算D
再把其中一个镜像翻转
反转后BAD会共线，从而退化成三角形。不再是四边形。
这个全等的证明我总结贴的前一贴有人已经给出来了。简单说连接BD，ABD是等腰三角形，两个底角角ABD和ADB相等，因原角B=角D，所以角CBD=角CDB，从而CB=CD，三边相等从而上下全等。这个题的一般情况其实是两个等腰三角形竖着贴在一起了。特殊情况是三点共线，从而不再是四边形，到的确不再是上下全等了。
hereyouare 写了： 2025年 11月 3日 02:54反转后BAD会共线，从而退化成三角形。不再是四边形。
这个全等的证明我总结贴的前一贴有人已经给出来了。简单说连接BD，ABD是等腰三角形，两个底角角ABD和ADB相等，因原角B=角D，所以角CBD=角CDB，从而CB=CD，三边相等从而上下全等。这个题的一般情况其实是两个等腰三角形竖着贴在一起了。特殊情况是三点共线，从而不再是四边形，到的确不再是上下全等了。
你说的对
纠正一下
是bcd贡献