图证勾股定理
发表于 ： 2023年 3月 4日 17:36
分页： 1 / 6
Re: 图证勾股定理
发表于 ： 2023年 3月 4日 22:44
还见到过好几个图证方法。
Re: 图证勾股定理
发表于 ： 2023年 3月 5日 09:35
中科院数学研究院的院徽，蕴含了两种勾股定理的证法：
这是最漂亮的两种证法，大家先猜猜看。
这是最漂亮的两种证法，大家先猜猜看。
Re: 图证勾股定理
发表于 ： 2023年 3月 5日 09:39
哦这个是(a+b)2=c2+2ab.
Re: 图证勾股定理
发表于 ： 2023年 3月 5日 10:45
里面的正方形是 |a - b|^2 + 2ab = c^2
Re: 图证勾股定理
发表于 ： 2023年 3月 5日 10:49
对！(a+b)2=c2+2ab是商高的证明（三千年前），（a - b）^2 + 2ab = c^2是赵爽的证明（两千年前），比欧几里得的证明强了不止一条街。
Re: 图证勾股定理
发表于 ： 2023年 3月 5日 10:54
哦！
呵呵。我想起大学时代的一件事，这是我自己经历的真事：有一天晚上我在教室自习，看见课桌文学写着一个谜语：宋美龄侧卧云床，打三国一人名。我想了一会儿，得到了答案：蒋干。其实我不擅长猜谜语。所以想出这个谜底我觉得很得意。回去告诉了宿舍的同学。
过了好几年，我上研究生的时候，宿舍里又有一帮同学，又提了这个谜语。我说了谜底是蒋干之后，他们告诉我这个谜语应该打三国两个人名。第二个是：庞统。
我拍案叫绝。
Re: 图证勾股定理
发表于 ： 2023年 3月 5日 11:07
不错，妙！TheMatrix 写了： 2023年 3月 5日 10:54 哦！
呵呵。我想起大学时代的一件事，这是我自己经历的真事：有一天晚上我在教室自习，看见课桌文学写着一个谜语：宋美龄侧卧云床，打三国一人名。我想了一会儿，得到了答案：蒋干。其实我不擅长猜谜语。所以想出这个谜底我觉得很得意。回去告诉了宿舍的同学。
过了好几年，我上研究生的时候，宿舍里又有一帮同学，又提了这个谜语。我说了谜底是蒋干之后，他们告诉我这个谜语应该打三国两个人名。第二个是：庞统。
我拍案叫绝。
Re: 图证勾股定理
发表于 ： 2023年 3月 5日 15:34
这和勾股定理有什么关系？
说中国古代没有证明的人，是无知。
说中国古代没有证明的人，是无知。
Re: 图证勾股定理
发表于 ： 2023年 3月 5日 17:50
三国时刘徽也有个证明：
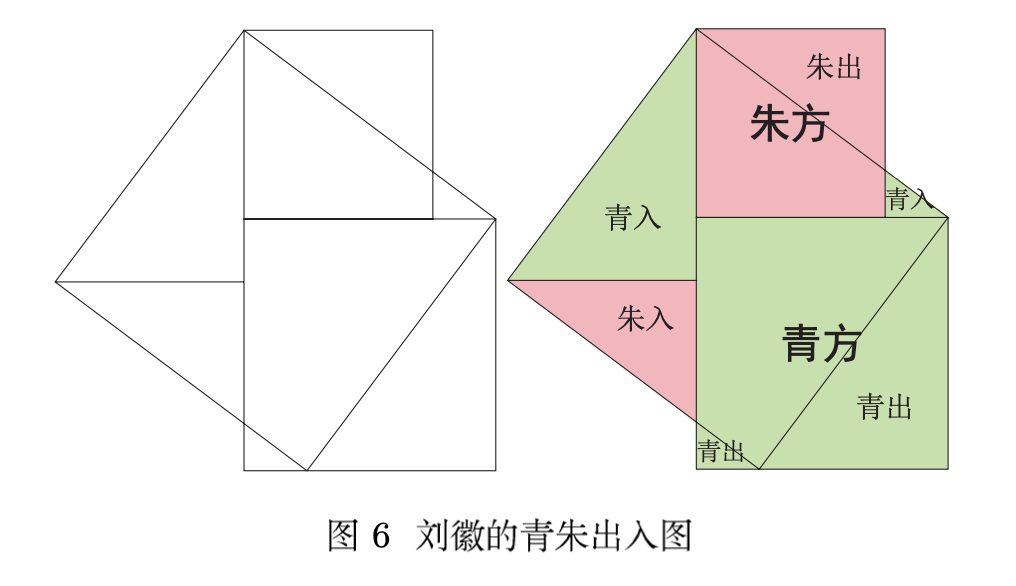
Re: 图证勾股定理
发表于 ： 2023年 3月 6日 03:00
Re: 图证勾股定理
发表于 ： 2023年 3月 6日 09:59
这大概是我中学时看到（学到）的第一个勾股定理的证明。说实话，我当时对这个证明不怎么感冒，觉得很繁杂、不明了，给我造成了一些阴影，使得我总以为勾股定理的证明很繁。
后来学了向斜边划垂线得到三个相似三角形，然后证出勾股定理，我觉得很好，很合我的思路，勾股定理证明的阴影才逐渐消除。
再后来又看到很多别的证明，包括中科院数学研究院的院徽，以及油管上很多证明，都令人称奇叫绝。
Re: 图证勾股定理
发表于 ： 2023年 3月 6日 11:31
对，这个证明比较繁琐，与顶楼类似。欧几里得的证明也有点繁琐。YWY 写了： 2023年 3月 6日 09:59 这大概是我中学时看到（学到）的第一个勾股定理的证明。说实话，我当时对这个证明不怎么感冒，觉得很繁杂、不明了，给我造成了一些阴影，使得我总以为勾股定理的证明很繁。
后来学了向斜边划垂线得到三个相似三角形，然后证出勾股定理，我觉得很好，很合我的思路，勾股定理证明的阴影才逐渐消除。
再后来又看到很多别的证明，包括中科院数学研究院的院徽，以及油管上很多证明，都令人称奇叫绝。
Re: 图证勾股定理
发表于 ： 2023年 3月 6日 11:44
我还记得，中学时看到的那个刘徽的证明，是画一个直角三角形，然后每个边向外画一个正方形，然后通过图的分割，演示两个小正方形的和等于大正方形的面积，如下图所示。虽然和你上面贴的异曲同工，但是要移动比对更多组面积，给我幼小心灵留下了阴影。
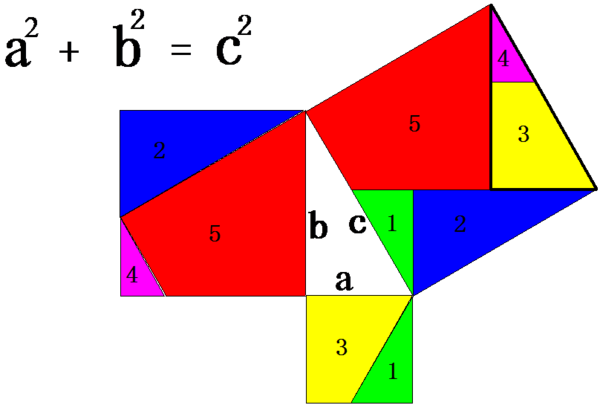
Re: 图证勾股定理
发表于 ： 2023年 3月 6日 11:49
这个不直观啊。把左上的图切成两半 一边转过来拼回去之后，中间的部分刚好是个边长为c的正方形，这一堆过程都得证明吧
Re: 图证勾股定理
发表于 ： 2023年 3月 6日 11:54
是。是要证明。我觉得要用相似三角形的证明。
Re: 图证勾股定理
发表于 ： 2023年 3月 6日 12:39
我觉得院徽那两个证明真是简单明了，一目了然。
我贴的那个动图很适合初学者
Re: 图证勾股定理
发表于 ： 2023年 3月 6日 12:49
所以我说商高和赵爽的证明是史上最漂亮的证明。这是白人抢credit的范例，毕达哥拉斯这个传说中的人物，连传说中都没有证明。