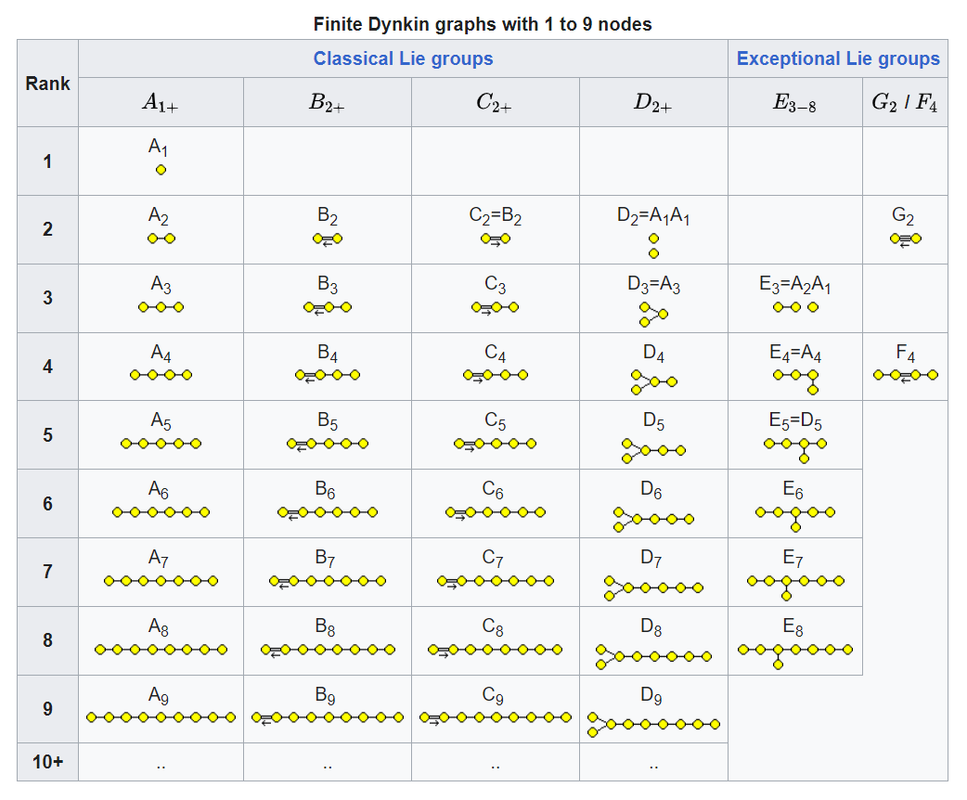
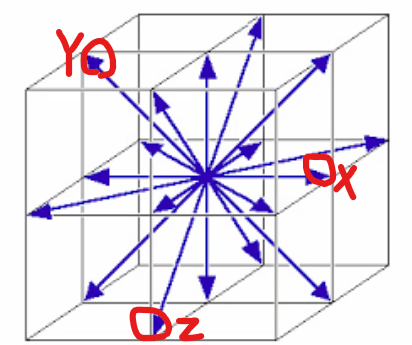
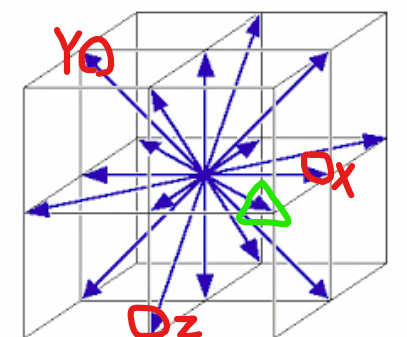
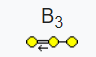#1 李代数
发表于 : 2024年 8月 31日 11:14
李代数从李群中来。李群是一个群同时也是一个manifold。是manifold就有tangent space。李代数是李群在单位元点的tagent space。这个tangent space不仅有vector space结构,还可以定义乘法。
这个乘法是从李群中导出的。李群一般是非交换群。也就是gh != hg,非交换的程度可以用一个commutator度量,也就是ghg-1h-1,相当于gh/(hg)。李群上的commutator线性化映射到李代数上,相当于变成了减法 dg dh - dh dg。也就是两个tangent vector dg 和 dh,组到一起,dg . dh = dg dh - dh dg,这就是李代数上的乘法,记为 [dg,dh]。
这都是不严格的记法。是一种形象化的记忆方法。这个应该是可以严格化的。但是挺费脑筋的。
从这个不严格的记法里看,显然有[dg,dh]=-[dh,dg],也有雅可比规则,[df,[dg,dh]]=[[df,dg],dh]+[dg,[df,dh]]。所以李代数的乘法既是非交换的,也不满足结合律。但是规则性还是很强的。
雅可比规则可以直接从[dg,dh]=dg dh - dh dg中推出。也和求导中的product rule有关。到底哪一个更本质我也没想好。
这些就是李代数的全部定义性质。所以也可以直接代数定义:
李代数就是一个vector space L,其上有一个乘法,记为 [a,b],要求满足:
[a,b]=-[b,a]
[a,[b,c]]=[[a,b],c]+[b,[a,c]]
这个乘法是从李群中导出的。李群一般是非交换群。也就是gh != hg,非交换的程度可以用一个commutator度量,也就是ghg-1h-1,相当于gh/(hg)。李群上的commutator线性化映射到李代数上,相当于变成了减法 dg dh - dh dg。也就是两个tangent vector dg 和 dh,组到一起,dg . dh = dg dh - dh dg,这就是李代数上的乘法,记为 [dg,dh]。
这都是不严格的记法。是一种形象化的记忆方法。这个应该是可以严格化的。但是挺费脑筋的。
从这个不严格的记法里看,显然有[dg,dh]=-[dh,dg],也有雅可比规则,[df,[dg,dh]]=[[df,dg],dh]+[dg,[df,dh]]。所以李代数的乘法既是非交换的,也不满足结合律。但是规则性还是很强的。
雅可比规则可以直接从[dg,dh]=dg dh - dh dg中推出。也和求导中的product rule有关。到底哪一个更本质我也没想好。
这些就是李代数的全部定义性质。所以也可以直接代数定义:
李代数就是一个vector space L,其上有一个乘法,记为 [a,b],要求满足:
[a,b]=-[b,a]
[a,[b,c]]=[[a,b],c]+[b,[a,c]]