新未名空间

数学家们和马工们请科普一下

可以

怎么实现的？

请讲讲原理

可以。傅里叶变换只是减少参数的数量而已。不会改变模型

我们文科生听不懂啊

这种演示确实比以前的教学方法好。

其实就是告诉你（一定条件下）复杂的函数可以看成简单的函数之和，这里的简单函数就是不同频率和振幅的正弦函数。

这是傅立叶极数吧

这个原理我听说过

具体怎么弄出来的？

还那么精确

只要级数够多就好，大一高数就教了，同济那个

画这个图的原理，就是地心说的本轮、均轮。不行就再加个轮。

据说傅里叶分析的傅里叶就是从这里得到的灵感。

verdelite 写了： 2022年 11月 10日 22:13 画这个图的原理，就是地心说的本轮、均轮。不行就再加个轮。

据说傅里叶分析的傅里叶就是从这里得到的灵感。

这个图是一个函数，还是多个函数分段？

AI 可以学一下！

TheMatrix2 写了： 2022年 11月 10日 22:26 这个图是一个函数，还是多个函数分段？

傅里叶分解，相当于多个函数叠加。不是分段，是叠加

verdelite 写了： 2022年 11月 10日 22:29 傅里叶分解，相当于多个函数叠加。不是分段，是叠加

哦，那就是一个函数 - 多个函数叠加还是一个函数。嗯，我也是这么感觉。这个视频我看过，但是没仔细看。

whatever you say

傅立叶变换是一种正交线性变换 。basis是复指数序列。跟这个图画有什么关系？

很多人智商有缺陷,
这些人眼中看到的世界是不一样的

比如下大雨,天上一道闪电滑过
智商有缺陷的人立马跪下叩头
口中说老天饶了我吧

你妈
你说你能这人交流闪电是怎么回事吗?
显然不能

sneezesnake 写了： 2022年 11月 11日 00:42 傅立叶变换是一种正交线性变换 。basis是复指数序列。跟这个图画有什么关系？

sneezesnake 写了： 2022年 11月 11日 00:42 傅立叶变换是一种正交线性变换 。basis是复指数序列。跟这个图画有什么关系？

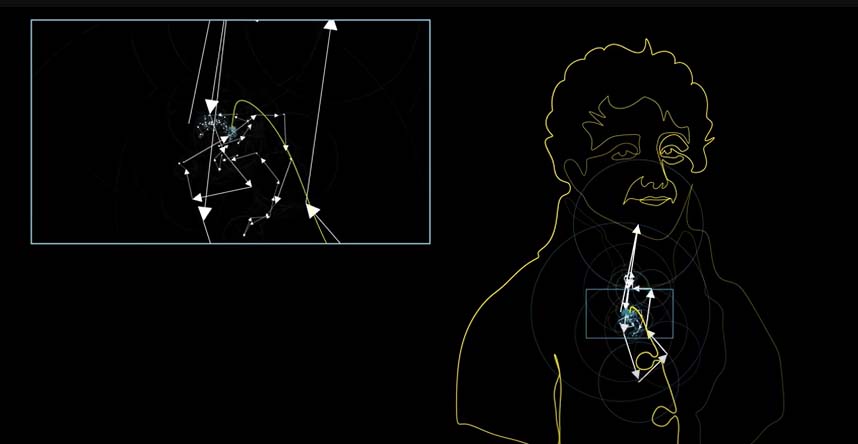
这个图是用一系列旋转的箭头画出来的。
这些连接的箭头其实就是矢量（复数）和，如果都旋转起来就是复变函数和。
旋转的速度对应频率，半径对应振幅。可以写成e^{jwt}或者e^-{jwt}的形式
所以这就是一个傅里叶级数的几何呈现。

如果频率w是有限个，那就只需要有限个e^{jwt}基，其和的形式就是傅里叶级数，等价于一个有限周期函数。
如果频率是无限个（不是有限周期函数），那就需要写成积分形式。所谓傅里叶变换就是通过与函数基进行内积而得到各频率成分的“权重”，是个关于频率的连续函数。
从这个意义上说，傅里叶逆变换就是傅里叶级数的一种形式。（或者傅里叶级数是有限周期函数的傅里叶逆变换）

一个简单的形式是e^{jt}+e^{-jt}，这就是一个余弦函数（2倍）
它的几何呈现是两个反向旋转的等长连结箭头，旋转周期2pi
如果有一条纸带随时间拉动，那画出来的就是余弦线。

画这个图是(x(t), y(t)), t是时间。x(t) 是个一维函数可以用傅立叶级数表示。a1 cos(t) + a2 cos(2t) + … 二维的话就用an cos(n t) 和 an sin(n t) 同时表示 x 和 y。就是很多周期不一样的圆

sneezesnake 写了： 2022年 11月 11日 00:42 傅立叶变换是一种正交线性变换 。basis是复指数序列。跟这个图画有什么关系？