#1 Navier-Stokes方程中的奇点
发表于 : 2025年 1月 18日 15:23
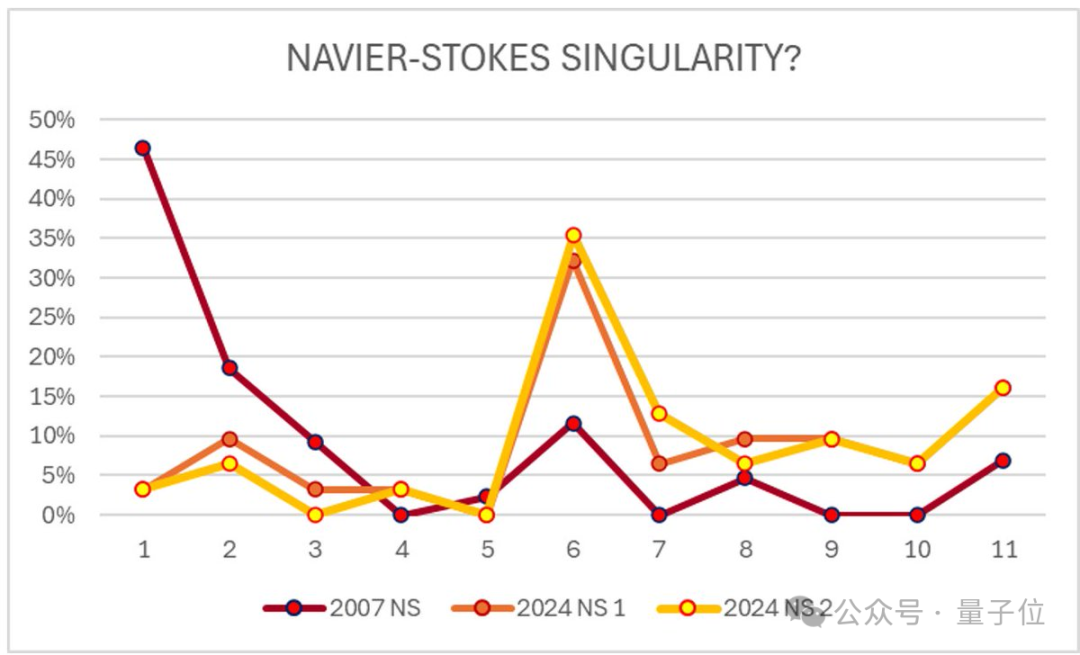
这是2024年一个数学会议上的投票。2007年做过同样的投票。结果显示,更多人比2007年更倾向于认为N-S方程中有奇点。
https://zhuanlan.zhihu.com/p/18666305633

https://zhuanlan.zhihu.com/p/18666305633




你完全miss了它 - 我那篇是哲学探讨。bouncingball 写了: 2025年 1月 18日 16:26 别显摆忽悠了,Navier流体方程木有问题。主要是Stokes本构方程是人为假设的(雷诺应力假设)。有本事你建立一套你自己的本构方程,看看还有木有奇点,嘿嘿!就跟隐式大涡模拟一样,人家就是自己建立了一套模型摆脱雷诺应力假设,嘿嘿!
Navier方程理论已经描述了真实世界,只是人们在实践过程中必须借助人为模型去模拟真实世界,这就是模拟世界和真实世界的误差,这个高等数学课的微积分精髓“分匀和精”早就阐明了这个哲学原理,这也叫新发现,嘿嘿!给你多点信息,除了Navier方程理论,还有玻尔兹曼方程理论,嘿嘿!格子玻尔兹曼就是人为建模求解玻尔兹曼方程的一种模型,此外还有蒙特卡洛模型,嘿嘿!
Navier-Stokes方程的建立,已经用了一些假设和简化,所以不能完全描述真实流体。我指的是这部分。bouncingball 写了: 2025年 1月 18日 18:32 Navier方程理论已经描述了真实世界,只是人们在实践过程中必须借助人为模型去模拟真实世界,这就是模拟世界和真实世界的误差,这个高等数学课的微积分精髓“分匀和精”早就阐明了这个哲学原理,这也叫新发现,嘿嘿!给你多点信息,除了Navier方程理论,还有玻尔兹曼方程理论,嘿嘿!格子玻尔兹曼就是人为建模求解玻尔兹曼方程的一种模型,此外还有蒙特卡洛模型,嘿嘿!
还有理论是可以描述真实世界的,但是要去具体求解或认知真实世界目前还离不开建模,一旦建模就有人为假设就会产生误差,这是科学。如果你说从这发现了哲学,那也不是什么新鲜的哲学。只能说知识面太窄,太缺乏了,嘿嘿!
Navier方程纯理论的流体方程是可以描述真实流体的,Stokes方程本构方程用了雷诺应力假设建模Navier方程的应力项。两个方程本来就不是一家,你非要说Navier-Stokes方程,这个方程已经不是用纯理论的流体方程描述真实流体了,当然不能完全描述真实流体,嘿嘿!但是不能说理论就不可以描述真实,嘿嘿!TheMatrix 写了: 2025年 1月 18日 19:59 Navier-Stokes方程的建立,已经用了一些假设和简化,所以不能完全描述真实流体。我指的是这部分。
求解的过程,当然可以再用简化。你指的是这部分。
bouncingball 写了: 2025年 1月 18日 20:11 Navier方程纯理论的流体方程是可以描述真实流体的,Stokes方程本构方程用了雷诺应力假设建模Navier方程的应力项。两个方程本来就不是一家,你非要说Navier-Stokes方程,这个方程已经不是用纯理论的流体方程描述真实流体了,当然不能完全描述真实流体,嘿嘿!但是不能说理论就不可以描述真实,嘿嘿!


TheMatrix 写了: 2025年 1月 18日 16:16 不过奇点解并不意味着真实流体中有奇点,而只意味着Navier-Stokes方程并不能完全描述真实流体。
同理,广义相对论如果有黑洞奇点解,也不意味着宇宙中真的有奇点,而只意味着爱因斯坦场方程不能完全描述真实的宇宙。