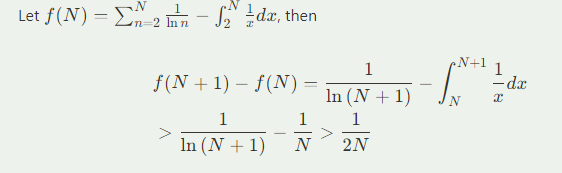lim N->∞ (Σ2N 1/ln(n) - ∫2N 1/ln(x) dx)
再加一问:
lim N->∞ (Σ 2N ln(n)-s - ∫2N ln(x)-s dx)
是不是s的解析函数?
求极限
版主: verdelite, TheMatrix
#2 Re: 求极限
Direct calculation gives
\sum_{2\leq n\leq N}1/(\log n)=\int_{2^{-}}^{N}1/(\log x)d[x]=\int_2^Ndx/(\log x)-int_{2^{-}}^N1/(\log x)d{x}=\int_2^Ndx/(\log x)-{x}/\logx|_{2^{-}}^N-int_2^Ndx/(x\log^2x)
where {x}=x-[x] is the fractional part of x. Thus, the limit wanted is equal to
1/\log2-int_2^{\infty}{x}/(x\log^2x)dx
The same argument shows that the second limit gives a function analytic on Re(s)>0.
\sum_{2\leq n\leq N}1/(\log n)=\int_{2^{-}}^{N}1/(\log x)d[x]=\int_2^Ndx/(\log x)-int_{2^{-}}^N1/(\log x)d{x}=\int_2^Ndx/(\log x)-{x}/\logx|_{2^{-}}^N-int_2^Ndx/(x\log^2x)
where {x}=x-[x] is the fractional part of x. Thus, the limit wanted is equal to
1/\log2-int_2^{\infty}{x}/(x\log^2x)dx
The same argument shows that the second limit gives a function analytic on Re(s)>0.
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13624
- 注册时间: 2022年 7月 26日 00:35
#3 Re: 求极限
format 一下:changbaihou 写了: 2024年 1月 3日 15:03 Direct calculation gives
\sum_{2\leq n\leq N}1/(\log n)=\int_{2^{-}}^{N}1/(\log x)d[x]=\int_2^Ndx/(\log x)-int_{2^{-}}^N1/(\log x)d{x}=\int_2^Ndx/(\log x)-{x}/\logx|_{2^{-}}^N-int_2^Ndx/(x\log^2x)
where {x}=x-[x] is the fractional part of x. Thus, the limit wanted is equal to
1/\log2-int_2^{\infty}{x}/(x\log^2x)dx
The same argument shows that the second limit gives a function analytic on Re(s)>0.

-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13624
- 注册时间: 2022年 7月 26日 00:35