几个练习题

[TheMatrix]

证明下面几个数在Z[√-5]中都是irreducible：{2,3,1+√-5,1-√-5} 。

[TheMatrix]

证明下面几个数在Z[√-5]中都是irreducible：{2,3,1+√-5,1-√-5} 。

我先来证明2是Z[√-5]的irreducible。

Z[√-5]可以embed到复数中看乘法。

Z[√-5]中，除了0之外，模最小的就是{1,-1}，所以这是全部的units。（units就是可逆元素）。

模次小的就是2了，以及和2相差units的，也就是{2,-2}。所以2是只能等于1*2。所以是irreducible。

再次小的就是√-5了，包括{√-5,-√-5}。

[TheMatrix]

我先来证明2是Z[√-5]的irreducible。

Z[√-5]可以embed到复数中看乘法。

Z[√-5]中，除了0之外，模最小的就是{1,-1}，所以这是全部的units。（units就是可逆元素）。

模次小的就是2了，以及和2相差units的，也就是{2,-2}。所以2是只能等于1*2。所以是irreducible。

再次小的就是√-5了，包括{√-5,-√-5}。

这里用到了复数的embedding，还有复数乘法，模的大小。这属于分析的方法了。

[FoxMe]

Z[√-5]这个环是很好的练习题。

要证明irreducible，看norm N(2)=4,N(3)=9,N(1+√-5)=6,N(1-√-5)=6。

而一般N(a-b√-5)=a²+5b²，检查整数解即可。

[FoxMe]

再出一题：证明3不是素元。

[TheMatrix]

再出一题：证明3不是素元。

3 is irreducible，这个可以用和证明“2”类似的方法 - 复数模的方法。

(3) is not a prime ideal，我用Z[√-5]/(3)不是integral domain来证明：

首先(3)里的元素是a+b√-5，其中a和b都能整除3。

所以Z[√-5]/(3)中的代表元为：
{0,1,2,
√-5,1+√-5,2+√-5,
2√-5,1+2√-5,2+2√-5}
共9个。

而其中(1+√-5)(1+2√-5)=-9+3√-5，系数能被3整除，所以在(3)中。

所以Z[√-5]/(3)不是integral domain。

[YWY]

我先来证明2是Z[√-5]的irreducible。

Z[√-5]可以embed到复数中看乘法。

Z[√-5]中，除了0之外，模最小的就是{1,-1}，所以这是全部的units。（units就是可逆元素）。

模次小的就是2了，以及和2相差units的，也就是{2,-2}。所以2是只能等于1*2。所以是irreducible。

再次小的就是√-5了，包括{√-5,-√-5}。

在Z[√-5]里，好像（正负）√-5是素元素，还能找到别的素元素吗？

[TheMatrix]

在Z[√-5]里，好像（正负）√-5是素元素，还能找到别的素元素吗？

你是说(√-5)是prime ideal？我看看。

“还有别的素元素吗”，不应该有很多吗？我知道Z[√-5]不是principal ideal domain，难道大部分的prime ideal都不是一个元素生成的？这还真没想过。我想想。

[TheMatrix]

Z[√-5]这个环是很好的练习题。

要证明irreducible，看norm N(2)=4,N(3)=9,N(1+√-5)=6,N(1-√-5)=6。

而一般N(a-b√-5)=a²+5b²，检查整数解即可。

嗯。N(√-5)=5，所以Z[√-5]/(√-5)有5个元素，所以是一个field。所以(√-5)是prime ideal。

N(a)怎么算出来的？哦我是问为什么N(a-b√-5)=a²+5b²？

[TheMatrix]

在Z[√-5]里，好像（正负）√-5是素元素，还能找到别的素元素吗？

如果按照FoxMe给出的norm公式的话，Z[√-5]/(a+b√-5)的元素个数等于N(a+b√-5)=a²+5b²。可以有很多个素数。也就是有很多(a+b√-5)是prime ideal。

[TheMatrix]

再出一题：证明3不是素元。

我再出一个问题。这个问题我想过也没想出来：

2在Z[√19]中是不是irreducible？注意这里是real quadratic。

(2)在Z[√19]中是不是prime ideal？

[TheMatrix]

我再出一个问题。这个问题我想过也没想出来：

2在Z[√19]中是不是irreducible？注意这里是real quadratic。

(2)在Z[√19]中是不是prime ideal？

这个问题可能只能用数论来证明了。embedding到复数中用模的方法不行了。因为a+b√19的模可以任意接近0。

[TheMatrix]

我再出一个问题。这个问题我想过也没想出来：

2在Z[√19]中是不是irreducible？注意这里是real quadratic。

(2)在Z[√19]中是不是prime ideal？

Z[√19]是principal ideal domain，因为Q[√19]的class number等于1（Wiki）。所以irreducible一定生成prime ideal。所以问题归结为2是不是irreducible。

[TheMatrix]

我再出一个问题。这个问题我想过也没想出来：

2在Z[√19]中是不是irreducible？注意这里是real quadratic。

(2)在Z[√19]中是不是prime ideal？

2 is not irreducible in Z[√19]。

试探法：(a+b√19)(-a+b√19)=2，有解：a=13, b=3。这个是Pell方程，有无穷多解。

[TheMatrix]

如果按照FoxMe给出的norm公式的话，Z[√-5]/(a+b√-5)的元素个数等于N(a+b√-5)=a²+5b²。可以有很多个素数。也就是有很多(a+b√-5)是prime ideal。

考虑x=2+3√-5，以及Z[√-5]/(x)的元素个数。N(x)=2²+5*3²=49。我们数以下看看是不是49个。

考虑Z[√-5]中的任意元素 a+b√-5，(a+b√-5)(2+3√-5)=(2a-15b)+(3a+2b)√-5。也就是这个形式的数都在(x)这个ideal之中。a,b可以取任意整数，那么格点(2a-15b,3a+2b)就是这个ideal中元素的系数可取的值。Z[√-5]/(x)就要看这个格点最小平行四边形中包含的整点数。



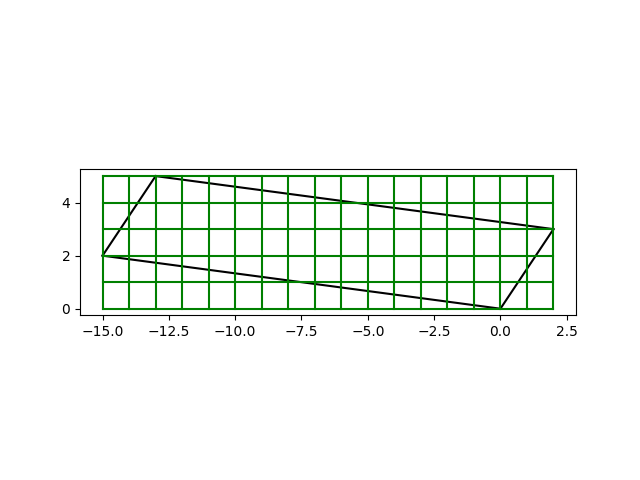
数了一下，确实是49个。信矣夫！

[TheMatrix]

考虑x=2+3√-5，以及Z[√-5]/(x)的元素个数。N(x)=2²+5*3²=49。我们数以下看看是不是49个。

考虑Z[√-5]中的任意元素 a+b√-5，(a+b√-5)(2+3√-5)=(2a-15b)+(3a+2b)√-5。也就是这个形式的数都在(x)这个ideal之中。a,b可以取任意整数，那么格点(2a-15b,3a+2b)就是这个ideal中元素的系数可取的值。Z[√-5]/(x)就要看这个格点最小平行四边形中包含的整点数。



数了一下，确实是49个。信矣夫！

对于任意x=a+b√-5，按照这个方法，其ideal最小平行四边形是两个向量张成的：(a,b)和(-5b,a)。其矩阵的determinant正是a²+5b²。是这么来的。里面还有一些细节。可信就好了。

[TheMatrix]

对于任意x=a+b√-5，按照这个方法，其ideal最小平行四边形是两个向量张成的：(a,b)和(-5b,a)。其矩阵的determinant正是a²+5b²。是这么来的。里面还有一些细节。可信就好了。

对于real二次扩域，比如Q[√19]，以及ring of integer Z[√19]，前面的操作都可以，得到的两个向量是(a,b)和(19b,a)，其矩阵的determinant是a²-19b²。不一定为正。这说明什么？

[FoxMe]

妙。同理可证2是素元：

Z[√-5]/(2)中的代表元为：{0,1,√-5,1+√-5}

3 is irreducible，这个可以用和证明“2”类似的方法 - 复数模的方法。

(3) is not a prime ideal，我用Z[√-5]/(3)不是integral domain来证明：

首先(3)里的元素是a+b√-5，其中a和b都能整除3。

所以Z[√-5]/(3)中的代表元为：
{0,1,2,
√-5,1+√-5,2+√-5,
2√-5,1+2√-5,2+2√-5}
共9个。

而其中(1+√-5)(1+2√-5)=-9+3√-5，系数能被3整除，所以在(3)中。

所以Z[√-5]/(3)不是integral domain。

[TheMatrix]

妙。同理可证2是素元：

Z[√-5]/(2)中的代表元为：{0,1,√-5,1+√-5}

2不是素元吧 - (2)不是prime ideal。

因为{0,1,√-5,1+√-5}这个ring是有zero divisor的。(1+√-5)(1+√-5)=-4+2√-5。在(2)中。

[FoxMe]

对，我弄错了。2是ramified。

那么剩下的(1+√-5)， (1+√-5)是不是素元？

2不是素元吧 - (2)不是prime ideal。

因为{0,1,√-5,1+√-5}这个ring是有zero divisor的。(1+√-5)(1+√-5)=-4+2√-5。在(2)中。