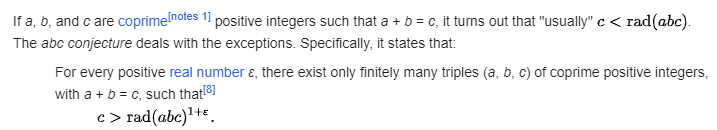abc conjecture
版主: verdelite, TheMatrix
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
#1 abc conjecture
就是量化表达一个现象。不是很容易量化,但是这个现象却是很明显,很容易表达。
假设有三个正整数,满足a+b=c,那么“一般来说”,有c < Rad(abc)。或者说,c > Rad(abc)的情况是“特例”。
Rad是Radical的缩写,中文翻译成“根式”。也就是分解质因数之后,把质因数的multiplicity去掉之后的数。比如x=4320=5*33*25,那么Rad(x)=5*3*2=30。
试验几个例子:
a=5,b=27,c=a+b=32
abc=5*27*32=5*33*25
Rad(abc)=5*3*2=30
Rad(abc) < c
这是特例。为什么是特例呢?因为随便变一个数:
a=5,b=28,c=a+b=33
abc=5*4*7*3*11
Rad(abc)=5*2*7*3*11
clearly, Rad(abc) > c
再变一个:
a=6,b=28,c=a+b=34
abc=2*3*4*7*2*17
Rad(abc)=2*3*7*17
还是clearly,Rad(abc) > c。
假设有三个正整数,满足a+b=c,那么“一般来说”,有c < Rad(abc)。或者说,c > Rad(abc)的情况是“特例”。
Rad是Radical的缩写,中文翻译成“根式”。也就是分解质因数之后,把质因数的multiplicity去掉之后的数。比如x=4320=5*33*25,那么Rad(x)=5*3*2=30。
试验几个例子:
a=5,b=27,c=a+b=32
abc=5*27*32=5*33*25
Rad(abc)=5*3*2=30
Rad(abc) < c
这是特例。为什么是特例呢?因为随便变一个数:
a=5,b=28,c=a+b=33
abc=5*4*7*3*11
Rad(abc)=5*2*7*3*11
clearly, Rad(abc) > c
再变一个:
a=6,b=28,c=a+b=34
abc=2*3*4*7*2*17
Rad(abc)=2*3*7*17
还是clearly,Rad(abc) > c。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
#2 Re: abc conjecture
这个现象非常容易让人相信。因为把a分解质因数,把b分解质因数,那么Rad(ab)就等于把a和b两个数的质因数乘到一起,这应该很大了,大于a+b也就是c,应该已经是很正常的事了,更别说Rad(abc) > c了。TheMatrix 写了: 2024年 5月 25日 21:08 就是量化表达一个现象。不是很容易量化,但是这个现象却是很明显,很容易表达。
假设有三个正整数,满足a+b=c,那么“一般来说”,有c < Rad(abc)。或者说,c > Rad(abc)的情况是“特例”。
“特例”在于几种情况:
a分解质因数会不会有很大的multiplicity,比如a=28*3=768,那么Rad(a)=2*3=6一下子变得很小。
b也是一样。
这里就涉及一个“整数的本质”:“随便”找一个数,multiplicity能很大吗?直觉上看是不能。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
#3 Re: abc conjecture
写到这里,似乎已经可以提炼出一个ab conjecture了。。。但是,似乎可以有系统性的方法欺骗这个想要量化表达的conjecture。所以再加上一个c=a+b。变成Rad(abc)>a+b。TheMatrix 写了: 2024年 5月 25日 21:40 这个现象非常容易让人相信。因为把a分解质因数,把b分解质因数,那么Rad(ab)就等于把a和b两个数的质因数乘到一起,这应该很大了,大于a+b也就是c,应该已经是很正常的事了,更别说Rad(abc) > c了。
“特例”在于几种情况:
a分解质因数会不会有很大的multiplicity,比如a=28*3=768,那么Rad(a)=2*3=6一下子变得很小。
b也是一样。
这里就涉及一个“整数的本质”:“随便”找一个数,multiplicity能很大吗?直觉上看是不能。
这里又涉及到一个“整数的本质”:加法对乘法是完全的“出其不意”。
我解释一下:
乘法对加法有分配律。分配律本质上是“线性”。c*(a+b)=c*a+c*b。这就是线性 - 线性代数中的线性。
而反过来,加法对乘法没有线性,c+(a*b) ?= (c+a)*(c+b)。
也可以这么看:把素数看成是整数乘法空间的一组基(basis)。分解质因数就是整数的基表示 - 几个2,几个3,几个7,这样的表示。那么加法作用在这个空间,不是线性的,而且是far from that。
再翻译回质因数的语言就是:(a+b)的质因数和a或b的质因数相比较,几乎没有任何规律 - 完全的“出其不意”。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
#4 Re: abc conjecture
a=2m, b=3n
这种情况差不多是最容易产生Rad(abc)<c的情况了。因为a和b质因数multiplicity比较大,它们的Radical又很小,等于2*3=6。只要c中有multiplicity,而且multiplicity的质因数大于等于7就行了。
还不少。下面是m,n<30的以上特例的列表:
(m,n)=(1, 5), c={5: 1, 7: 2}
(m,n)=(9, 3), c={7: 2, 11: 1}
(m,n)=(11, 2), c={11: 2, 17: 1}
(m,n)=(6, 9), c={7: 2, 13: 1, 31: 1}
(m,n)=(14, 2), c={13: 2, 97: 1}
(m,n)=(1, 16), c={19: 2, 119243: 1}
(m,n)=(7, 10), c={17: 1, 59: 2}
(m,n)=(10, 7), c={13: 2, 19: 1}
(m,n)=(3, 15), c={5: 1, 7: 2, 58567: 1}
(m,n)=(6, 12), c={5: 1, 13: 2, 17: 1, 37: 1}
(m,n)=(11, 7), c={5: 1, 7: 1, 11: 2}
(m,n)=(17, 1), c={5: 2, 7: 2, 107: 1}
(m,n)=(2, 17), c={13: 2, 764143: 1}
(m,n)=(14, 7), c={7: 2, 379: 1}
(m,n)=(11, 12), c={11: 2, 4409: 1}
(m,n)=(11, 13), c={7: 2, 32579: 1}
(m,n)=(8, 19), c={7: 2, 37: 1, 643: 1, 997: 1}
(m,n)=(22, 5), c={7: 4, 1747: 1}
(m,n)=(25, 2), c={41: 2, 19961: 1}
(m,n)=(11, 17), c={11: 2, 97: 1, 11003: 1}
这种情况差不多是最容易产生Rad(abc)<c的情况了。因为a和b质因数multiplicity比较大,它们的Radical又很小,等于2*3=6。只要c中有multiplicity,而且multiplicity的质因数大于等于7就行了。
还不少。下面是m,n<30的以上特例的列表:
(m,n)=(1, 5), c={5: 1, 7: 2}
(m,n)=(9, 3), c={7: 2, 11: 1}
(m,n)=(11, 2), c={11: 2, 17: 1}
(m,n)=(6, 9), c={7: 2, 13: 1, 31: 1}
(m,n)=(14, 2), c={13: 2, 97: 1}
(m,n)=(1, 16), c={19: 2, 119243: 1}
(m,n)=(7, 10), c={17: 1, 59: 2}
(m,n)=(10, 7), c={13: 2, 19: 1}
(m,n)=(3, 15), c={5: 1, 7: 2, 58567: 1}
(m,n)=(6, 12), c={5: 1, 13: 2, 17: 1, 37: 1}
(m,n)=(11, 7), c={5: 1, 7: 1, 11: 2}
(m,n)=(17, 1), c={5: 2, 7: 2, 107: 1}
(m,n)=(2, 17), c={13: 2, 764143: 1}
(m,n)=(14, 7), c={7: 2, 379: 1}
(m,n)=(11, 12), c={11: 2, 4409: 1}
(m,n)=(11, 13), c={7: 2, 32579: 1}
(m,n)=(8, 19), c={7: 2, 37: 1, 643: 1, 997: 1}
(m,n)=(22, 5), c={7: 4, 1747: 1}
(m,n)=(25, 2), c={41: 2, 19961: 1}
(m,n)=(11, 17), c={11: 2, 97: 1, 11003: 1}
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
#5 Re: abc conjecture
漏了一些情况:TheMatrix 写了: 2024年 5月 26日 11:33 a=2m, b=3n
这种情况差不多是最容易产生Rad(abc)<c的情况了。因为a和b质因数multiplicity比较大,它们的Radical又很小,等于2*3=6。只要c中有multiplicity,而且multiplicity的质因数大于等于7就行了。
还不少。下面是m,n<30的以上特例的列表:
(m,n)=(1, 5), c={5: 1, 7: 2}
(m,n)=(9, 3), c={7: 2, 11: 1}
(m,n)=(11, 2), c={11: 2, 17: 1}
(m,n)=(6, 9), c={7: 2, 13: 1, 31: 1}
(m,n)=(14, 2), c={13: 2, 97: 1}
(m,n)=(1, 16), c={19: 2, 119243: 1}
(m,n)=(7, 10), c={17: 1, 59: 2}
(m,n)=(10, 7), c={13: 2, 19: 1}
(m,n)=(3, 15), c={5: 1, 7: 2, 58567: 1}
(m,n)=(6, 12), c={5: 1, 13: 2, 17: 1, 37: 1}
(m,n)=(11, 7), c={5: 1, 7: 1, 11: 2}
(m,n)=(17, 1), c={5: 2, 7: 2, 107: 1}
(m,n)=(2, 17), c={13: 2, 764143: 1}
(m,n)=(14, 7), c={7: 2, 379: 1}
(m,n)=(11, 12), c={11: 2, 4409: 1}
(m,n)=(11, 13), c={7: 2, 32579: 1}
(m,n)=(8, 19), c={7: 2, 37: 1, 643: 1, 997: 1}
(m,n)=(22, 5), c={7: 4, 1747: 1}
(m,n)=(25, 2), c={41: 2, 19961: 1}
(m,n)=(11, 17), c={11: 2, 97: 1, 11003: 1}
case 1: (m,n)=(1, 5), c={5: 1, 7: 2}
case 1: (m,n)=(9, 3), c={7: 2, 11: 1}
case 1: (m,n)=(11, 2), c={11: 2, 17: 1}
case 2: (m,n)=(6, 8), c={5: 3, 53: 1}
case 1: (m,n)=(6, 9), c={7: 2, 13: 1, 31: 1}
case 1: (m,n)=(14, 2), c={13: 2, 97: 1}
case 1: (m,n)=(1, 16), c={19: 2, 119243: 1}
case 1: (m,n)=(7, 10), c={17: 1, 59: 2}
case 1: (m,n)=(10, 7), c={13: 2, 19: 1}
case 1: (m,n)=(3, 15), c={5: 1, 7: 2, 58567: 1}
case 1: (m,n)=(6, 12), c={5: 1, 13: 2, 17: 1, 37: 1}
case 1: (m,n)=(11, 7), c={5: 1, 7: 1, 11: 2}
case 1: (m,n)=(17, 1), c={5: 2, 7: 2, 107: 1}
case 1: (m,n)=(2, 17), c={13: 2, 764143: 1}
case 1: (m,n)=(14, 7), c={7: 2, 379: 1}
case 2: (m,n)=(13, 9), c={5: 3, 223: 1}
case 1: (m,n)=(11, 12), c={11: 2, 4409: 1}
case 1: (m,n)=(11, 13), c={7: 2, 32579: 1}
case 2: (m,n)=(4, 22), c={5: 3, 13781: 1, 18217: 1}
case 1: (m,n)=(8, 19), c={7: 2, 37: 1, 643: 1, 997: 1}
case 1: (m,n)=(22, 5), c={7: 4, 1747: 1}
case 1: (m,n)=(25, 2), c={41: 2, 19961: 1}
case 1: (m,n)=(11, 17), c={11: 2, 97: 1, 11003: 1}
-
Caravel
- 论坛元老

Caravel 的博客 - 帖子互动: 685
- 帖子: 27166
- 注册时间: 2022年 7月 24日 17:21
#6 Re: abc conjecture
这么多例外,为啥还叫定理?TheMatrix 写了: 2024年 5月 26日 11:47 漏了一些情况:
case 1: (m,n)=(1, 5), c={5: 1, 7: 2}
case 1: (m,n)=(9, 3), c={7: 2, 11: 1}
case 1: (m,n)=(11, 2), c={11: 2, 17: 1}
case 2: (m,n)=(6, 8), c={5: 3, 53: 1}
case 1: (m,n)=(6, 9), c={7: 2, 13: 1, 31: 1}
case 1: (m,n)=(14, 2), c={13: 2, 97: 1}
case 1: (m,n)=(1, 16), c={19: 2, 119243: 1}
case 1: (m,n)=(7, 10), c={17: 1, 59: 2}
case 1: (m,n)=(10, 7), c={13: 2, 19: 1}
case 1: (m,n)=(3, 15), c={5: 1, 7: 2, 58567: 1}
case 1: (m,n)=(6, 12), c={5: 1, 13: 2, 17: 1, 37: 1}
case 1: (m,n)=(11, 7), c={5: 1, 7: 1, 11: 2}
case 1: (m,n)=(17, 1), c={5: 2, 7: 2, 107: 1}
case 1: (m,n)=(2, 17), c={13: 2, 764143: 1}
case 1: (m,n)=(14, 7), c={7: 2, 379: 1}
case 2: (m,n)=(13, 9), c={5: 3, 223: 1}
case 1: (m,n)=(11, 12), c={11: 2, 4409: 1}
case 1: (m,n)=(11, 13), c={7: 2, 32579: 1}
case 2: (m,n)=(4, 22), c={5: 3, 13781: 1, 18217: 1}
case 1: (m,n)=(8, 19), c={7: 2, 37: 1, 643: 1, 997: 1}
case 1: (m,n)=(22, 5), c={7: 4, 1747: 1}
case 1: (m,n)=(25, 2), c={41: 2, 19961: 1}
case 1: (m,n)=(11, 17), c={11: 2, 97: 1, 11003: 1}
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
#8 Re: abc conjecture
除了望月新一号称证明了ABC猜想之外,目前最好的结果是Stewart和于坤瑞的:
Stewart, C. L.; Yu, Kunrui (1991). "On the abc conjecture". Mathematische Annalen. 291 (1): 225–230. doi:10.1007/BF01445201. S2CID 123894587.
Stewart, C. L.; Yu, Kunrui (2001). "On the abc conjecture, II". Duke Mathematical Journal. 108 (1): 169–181. doi:10.1215/S0012-7094-01-10815-6.
他们只证明了类似c < exp(rad(abc))这种指数界,离猜想相差很远。
Stewart, C. L.; Yu, Kunrui (1991). "On the abc conjecture". Mathematische Annalen. 291 (1): 225–230. doi:10.1007/BF01445201. S2CID 123894587.
Stewart, C. L.; Yu, Kunrui (2001). "On the abc conjecture, II". Duke Mathematical Journal. 108 (1): 169–181. doi:10.1215/S0012-7094-01-10815-6.
他们只证明了类似c < exp(rad(abc))这种指数界,离猜想相差很远。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
#9 Re: abc conjecture
搜了一下。看到这样一个文章:FoxMe 写了: 2024年 5月 26日 16:27 除了望月新一号称证明了ABC猜想之外,目前最好的结果是Stewart和于坤瑞的:
Stewart, C. L.; Yu, Kunrui (1991). "On the abc conjecture". Mathematische Annalen. 291 (1): 225–230. doi:10.1007/BF01445201. S2CID 123894587.
Stewart, C. L.; Yu, Kunrui (2001). "On the abc conjecture, II". Duke Mathematical Journal. 108 (1): 169–181. doi:10.1215/S0012-7094-01-10815-6.
他们只证明了类似c < exp(rad(abc))这种指数界,离猜想相差很远。

-
Caravel
- 论坛元老

Caravel 的博客 - 帖子互动: 685
- 帖子: 27166
- 注册时间: 2022年 7月 24日 17:21
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
-
Caravel
- 论坛元老

Caravel 的博客 - 帖子互动: 685
- 帖子: 27166
- 注册时间: 2022年 7月 24日 17:21
#12 Re: abc conjecture
现在数学一个领域就是那么几个专家看的懂,据说Hamilton认为Pereman的庞加莱猜想不对,还在自己弄。老一点的专家比如老邱连仔细看一遍论文的力气都没有了。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
#13 Re: abc conjecture
陶哲轩在搞的机器证明可能会有帮助。陶哲轩搞的实际上是帮人把证明写出来的那种机器证明。Caravel 写了: 2024年 5月 27日 12:21 现在数学一个领域就是那么几个专家看的懂,据说Hamilton认为Pereman的庞加莱猜想不对,还在自己弄。老一点的专家比如老邱连仔细看一遍论文的力气都没有了。
还有就是,真正重要的证明,或者方法,一定会被很多人掰开了揉碎了仔细讲。费马大定理的证明差不多是这种情况了。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
#14 Re: abc conjecture
线性就是respect结构。TheMatrix 写了: 2024年 5月 25日 22:13 我解释一下:
乘法对加法有分配律。分配律本质上是“线性”。c*(a+b)=c*a+c*b。这就是线性 - 线性代数中的线性。
而反过来,加法对乘法没有线性,c+(a*b) ?= (c+a)*(c+b)。
也可以这么看:把素数看成是整数乘法空间的一组基(basis)。分解质因数就是整数的基表示 - 几个2,几个3,几个7,这样的表示。那么加法作用在这个空间,不是线性的,而且是far from that。
f(a+b) = f(a) + f(b)
{a,b} ---f---> {f(a),f(b)}
在左边加,和在右边加,结果是一样的 - 这就是respect加法结构。
所以乘法respect加法结构,而加法不respect乘法结构。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35
#15 Re: abc conjecture
所以以前有人问过一个问题 - 我自己也问过这个问题 - 有没有三层二元运算的代数结构,一层对下一层有分配律。TheMatrix 写了: 2024年 5月 28日 21:10 线性就是respect结构。
f(a+b) = f(a) + f(b)
{a,b} ---f---> {f(a),f(b)}
在左边加,和在右边加,结果是一样的 - 这就是respect加法结构。
所以乘法respect加法结构,而加法不respect乘法结构。
可以这么考虑。起始于一个ring R,自带两层结构,加法和乘法,乘法对加法有分配律。
再考虑ring homomorphism集合 Hom(R) = {f: R --> R}。
f(ab) = f(a)f(b)
a(b+c)=ab+ac
这就是两层分配律了。
所以问题就在于构造一个 Hom(R) --> R的映射了。
有点幂集映射回集合的意思了。
#16 Re: abc conjecture
我觉得可以先搞证明核对,这样就可以判断望月新一的证明到底对不对。
TheMatrix 写了: 2024年 5月 27日 16:03 陶哲轩在搞的机器证明可能会有帮助。陶哲轩搞的实际上是帮人把证明写出来的那种机器证明。
还有就是,真正重要的证明,或者方法,一定会被很多人掰开了揉碎了仔细讲。费马大定理的证明差不多是这种情况了。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13625
- 注册时间: 2022年 7月 26日 00:35