STEM版,合并数学,物理,化学,科学,工程,机械。不包括生物、医学相关,和计算机相关内容。
版主: verdelite, TheMatrix
-
(ヅ)楼主
- 论坛支柱

- 帖子互动: 549
- 帖子: 11819
- 注册时间: 2022年 8月 21日 14:20
帖子
由 (ヅ)楼主 »
-
verdelite
- 论坛元老

- 帖子互动: 1034
- 帖子: 24215
- 注册时间: 2022年 7月 21日 23:33
帖子
由 verdelite »
你这个问题的解答:网站的解答是对的,描述的是杆的质心的平动方程,直接可以使用牛顿第二定律。然后,利用加速度的线性叠加原理可以直接得出网站的解答。
而你给出的疑问,似乎是想要先写出质心坐标,然后求导两次得到质心加速度。但是你给的x cos (theta) 不知道是个啥,并非质心坐标。如果你硬要用坐标再求导两次的做法,我写了个过程,比原方法繁琐很多,但是也得到正确答案。一会儿上图。
图来了(注意图上第八行最后一项符号写错了):
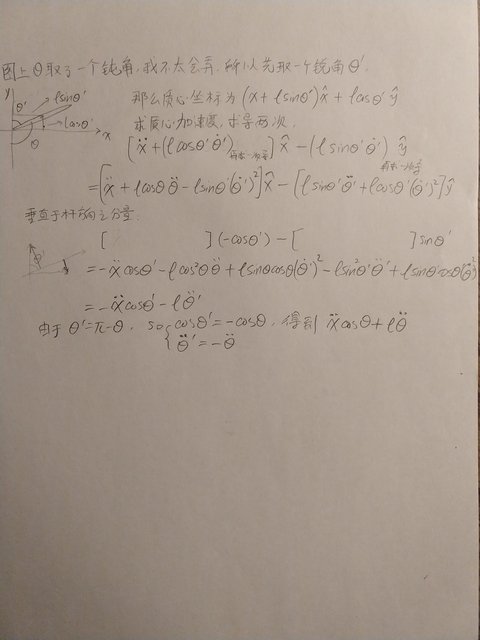
-
(ヅ)楼主
- 论坛支柱

- 帖子互动: 549
- 帖子: 11819
- 注册时间: 2022年 8月 21日 14:20
帖子
由 (ヅ)楼主 »
verdelite 写了: 2022年 11月 12日 22:39
你这个问题的解答:网站的解答是对的,描述的是杆的质心的平动方程,直接可以使用牛顿第二定律。然后,利用加速度的线性叠加原理可以直接得出网站的解答。
而你给出的疑问,似乎是想要先写出质心坐标,然后求导两次得到质心加速度。但是你给的x cos (theta) 不知道是个啥,并非质心坐标。如果你硬要用坐标再求导两次的做法,我写了个过程,比原方法繁琐很多,但是也得到正确答案。一会儿上图。
x cos(theta)是cart带着杆的水平运动,在垂直杆的方向上的分量
-
verdelite
- 论坛元老

- 帖子互动: 1034
- 帖子: 24215
- 注册时间: 2022年 7月 21日 23:33
帖子
由 verdelite »
(ヅ) 写了: 2022年 11月 12日 22:45
x cos(theta)是cart带着杆的水平运动,在垂直杆的方向上的分量
你这思维不清楚,估计是概念有问题。比如:“运动”是什么意思?是某一点(哪一点?)的坐标,速度,还是加速度?
看我补充的图有详细解答。
-
(ヅ)楼主
- 论坛支柱

- 帖子互动: 549
- 帖子: 11819
- 注册时间: 2022年 8月 21日 14:20
帖子
由 (ヅ)楼主 »
verdelite 写了: 2022年 11月 12日 22:53
你这思维不清楚,估计是概念有问题。比如:“运动”是什么意思?是某一点(哪一点?)的坐标,速度,还是加速度?
看我补充的图有详细解答。
摆在垂直摆这个方向的运动,为什么不能看成是摆的转动的切线方向和车带来的速度在这个方向上的叠加
-
verdelite
- 论坛元老

- 帖子互动: 1034
- 帖子: 24215
- 注册时间: 2022年 7月 21日 23:33
帖子
由 verdelite »
(ヅ) 写了: 2022年 11月 12日 22:59
摆在垂直摆这个方向的运动,为什么不能看成是摆的转动的切线方向和车带来的速度在这个方向上的叠加
你如果想用对速度求导的方法得到加速度,也行。结果会是一样。
但是得注意,加速度方向并不总是平行于速度方向(例如简单的圆形轨道行星运动的加速度方向指向圆心,和速度方向垂直)。考虑这个因素后,速度求导得到加速度,然后再求分量,才是对的。
-
弃婴千枝
- 论坛支柱

- 帖子互动: 1402
- 帖子: 13447
- 注册时间: 2022年 7月 27日 10:51
帖子
由 弃婴千枝 »
因为这是非惯性参照系,
非惯性参照系引入的虚拟力是纯粹水平方向的(题目最前面假定),
第一项是本系统实体力,
第二项是非惯性系引入的虚拟力,
所以虚拟力作用到倒立摆上的分力只能用mx'' cos(theta),
而不是m(x cos(theta))''
如果用m(x cos(theta))''就会否定最前面小车只局限与水平直线运动的假设
(本质上,虚拟力导数遵循偏导数而不是全微分,这个是深入的pholsophical question,我估计你的困惑在这里,你需要深入想想为什么)
你妈,一帮傻叉吐沫横飞,说那么多,总是抓不住关键核心
上次由 弃婴千枝 在 2022年 11月 12日 23:55 修改。
-
(ヅ)楼主
- 论坛支柱

- 帖子互动: 549
- 帖子: 11819
- 注册时间: 2022年 8月 21日 14:20
帖子
由 (ヅ)楼主 »
弃婴千枝 写了: 2022年 11月 12日 23:50
因为这是非惯性参照系,
非惯性参照系引入的虚拟力是纯粹水平方向的(题目最前面假定),
第一项是本系统实体力,
第二项是非惯性系引入的虚拟力,
所以虚拟力作用到倒立摆上的分力只能用mx'' cos(theta),
而不是m(x cos(theta))''
如果用m(x cos(theta))''就会否定最前面小车只局限与水平直线运动的假设
你妈,一帮傻叉吐沫横飞,说那么多,总是抓不住关键核心
感谢我的分身解答
非惯性系里面是不是补偿一个加速度就可以按照惯性系来写牛二方程了?
-
弃婴千枝
- 论坛支柱

- 帖子互动: 1402
- 帖子: 13447
- 注册时间: 2022年 7月 27日 10:51
帖子
由 弃婴千枝 »
本质上,虚拟力导数遵循偏导数而不是全微分,这个是深入的pholsophical question,我估计你的困惑在这里,你需要深入想想为什么
虚拟力的任何作用都是\partial,而不是d
(ヅ) 写了: 2022年 11月 12日 23:55
感谢我的分身解答
非惯性系里面是不是补偿一个加速度就可以按照惯性系来写牛二方程了?
-
弃婴千枝
- 论坛支柱

- 帖子互动: 1402
- 帖子: 13447
- 注册时间: 2022年 7月 27日 10:51
帖子
由 弃婴千枝 »
补偿反方向惯性力
(ヅ) 写了: 2022年 11月 12日 23:55
感谢我的分身解答
非惯性系里面是不是补偿一个加速度就可以按照惯性系来写牛二方程了?
-
(ヅ)楼主
- 论坛支柱

- 帖子互动: 549
- 帖子: 11819
- 注册时间: 2022年 8月 21日 14:20
帖子
由 (ヅ)楼主 »
弃婴千枝 写了: 2022年 11月 12日 23:56
本质上,虚拟力导数遵循偏导数而不是全微分,这个是深入的pholsophical question,我估计你的困惑在这里,你需要深入想想为什么
虚拟力的任何作用都是\partial,而不是d
超出我能力范围了,但是知道了之前的想法问题在哪里,学到一个技能点
-
弃婴千枝
- 论坛支柱

- 帖子互动: 1402
- 帖子: 13447
- 注册时间: 2022年 7月 27日 10:51
帖子
由 弃婴千枝 »
问题就是出现了水平方向的虚拟力,这个虚拟力可以看成水平方向的重力,跟重力一样方式处理(作用都是\partial 不是d),所以不能对角度求全微分,这样违反虚拟力作用准则
(ヅ) 写了: 2022年 11月 12日 23:58
超出我能力范围了,但是知道了之前的想法问题在哪里,学到一个技能点
x1

-
verdelite
- 论坛元老

- 帖子互动: 1034
- 帖子: 24215
- 注册时间: 2022年 7月 21日 23:33
帖子
由 verdelite »
(ヅ) 写了: 2022年 11月 12日 23:58
超出我能力范围了,但是知道了之前的想法问题在哪里,学到一个技能点
虚拟力的本质是个short cut,比赛做题速度的时候有用。多记住好几个东西,浪费脑细胞,还要经常练习。
我前面给出的解法是降龙十八掌那样的,需要记忆的东西少,而且也不一定快,但是保证能做出来。
-
弃婴千枝
- 论坛支柱

- 帖子互动: 1402
- 帖子: 13447
- 注册时间: 2022年 7月 27日 10:51
帖子
由 弃婴千枝 »
嘴硬有个鸡巴用
你根本理解不了楼主的困惑在哪里
你妈,楼主的困惑就是为啥不用全导数而用了偏导数,
你不理解楼主的困惑是因为你自己也不明白
稀里糊涂用了别的方法来绕开直接面对楼主的困惑
这好像有人问windows里面的这个设置怎么办的时候
总有傻逼跳出来说用linux就没这个问题了
你妈,人问的是windows里面怎么解答,
人对linux不感兴趣
verdelite 写了: 2022年 11月 13日 00:07
虚拟力的本质是个short cut,比赛做题速度的时候有用。多记住好几个东西,浪费脑细胞,还要经常练习。
我前面给出的解法是降龙十八掌那样的,需要记忆的东西少,而且也不一定快,但是保证能做出来。
x1

-
verdelite
- 论坛元老

- 帖子互动: 1034
- 帖子: 24215
- 注册时间: 2022年 7月 21日 23:33
帖子
由 verdelite »
弃婴千枝 写了: 2022年 11月 13日 00:42
嘴硬有个鸡巴用
你根本理解不了楼主的困惑在哪里
你妈,楼主的困惑就是为啥不用全导数而用了偏导数,
你不理解楼主的困惑是因为你自己也不明白
稀里糊涂用了别的方法来绕开直接面对楼主的困惑
这好像有人问windows里面的这个设置怎么办的时候
总有傻逼跳出来说用linux就没这个问题了
你妈,人问的是windows里面怎么解答,
人对linux不感兴趣
我确实不明白他在干啥。在我看来他就是概念不清、含糊地使用“运动”一词。
为啥我不用虚拟力?因为我现在搞的东西涉及狭义相对论,会避开这种牛顿力学下的short cuts。
-
YWY(夜未央)
- 论坛元老

2023-24年度十大优秀网友
- 帖子互动: 1331
- 帖子: 14346
- 注册时间: 2022年 7月 22日 17:25
帖子
由 YWY(夜未央) »
用mx'' cos(theta),是因为cart施加给InvertedPendulum的力总共是mx'',分解到与InvertedPendulum垂直的方向,就得到mx'' cos(theta)。
你说的m(x cos(theta))''只对应x cos(theta)这个矢量的二阶导(加速度),而且此时你必须把x cos(theta)当做矢量考虑,注意x cos(theta)的二阶导的方向(矢量的导数还是矢量)还不一定垂直于InvertedPendulum,所以还要再做一次分解。再就是,x cos(theta)只是cart给InvertedPendulum的驱动的一部分(全部是x),所以还需考虑(x - x cos(theta))做为矢量差的二阶导然后做相应方向的分解。两个二阶导全考虑了之后(包括做垂直于InvertedPendulum方向的分解之后),你注意到,加起来其实就是x的二阶导然后做垂直于InvertedPendulum方向的分解,也就是x'' cos(theta),因为x'' = (x cos(theta))'' + (x - x cos(theta))''。所以,莫不如你一开始就直接考虑x'',既简单又省事。
x1

持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
YWY(夜未央)
- 论坛元老

2023-24年度十大优秀网友
- 帖子互动: 1331
- 帖子: 14346
- 注册时间: 2022年 7月 22日 17:25
帖子
由 YWY(夜未央) »
YWY 写了: 2022年 11月 13日 11:08
用mx'' cos(theta),是因为cart施加给InvertedPendulum的力总共是mx'',分解到与InvertedPendulum垂直的方向,就得到mx'' cos(theta)。
你说的m(x cos(theta))''只对应x cos(theta)这个矢量的二阶导(加速度),而且此时你必须把x cos(theta)当做矢量考虑,注意x cos(theta)的二阶导的方向(矢量的导数还是矢量)还不一定垂直于InvertedPendulum,所以还要再做一次分解。再就是,x cos(theta)只是cart给InvertedPendulum的驱动的一部分(全部是x),所以还需考虑(x - x cos(theta))做为矢量差的二阶导然后做相应方向的分解。两个二阶导全考虑了之后(包括做垂直于InvertedPendulum方向的分解之后),你注意到,加起来其实就是x的二阶导然后做垂直于InvertedPendulum方向的分解,也就是x'' cos(theta),因为x'' = (x cos(theta))'' + (x - x cos(theta))''。所以,莫不如你一开始就直接考虑x'',既简单又省事。
注意,我上面x cos(theta)代表的是向量x在垂直于InvertedPendulum方向的分解(投影),不表示cos(theta)和x的数量积,其方向当然和x也不同。严格来说x cos(theta)这个表示是不对的。
总之,先分解x然后再求导是舍近求远费二遍事,直接对 x求导简单省事。
还有,这都是对时间求导,谈不上偏导数。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
(ヅ)楼主
- 论坛支柱

- 帖子互动: 549
- 帖子: 11819
- 注册时间: 2022年 8月 21日 14:20
帖子
由 (ヅ)楼主 »
YWY 写了: 2022年 11月 13日 11:37
注意,我上面x cos(theta)代表的是向量x在垂直于InvertedPendulum方向的分解(投影),不表示cos(theta)和x的数量积,其方向当然和x也不同。严格来说x cos(theta)这个表示是不对的。
总之,先分解x然后再求导是舍近求远费二遍事,直接对 x求导简单省事。
还有,这都是对时间求导,谈不上偏导数。
我仔细看看,谢谢!