李代数
版主: verdelite, TheMatrix
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13633
- 注册时间: 2022年 7月 26日 00:35
#1 李代数
李代数从李群中来。李群是一个群同时也是一个manifold。是manifold就有tangent space。李代数是李群在单位元点的tagent space。这个tangent space不仅有vector space结构,还可以定义乘法。
这个乘法是从李群中导出的。李群一般是非交换群。也就是gh != hg,非交换的程度可以用一个commutator度量,也就是ghg-1h-1,相当于gh/(hg)。李群上的commutator线性化映射到李代数上,相当于变成了减法 dg dh - dh dg。也就是两个tangent vector dg 和 dh,组到一起,dg . dh = dg dh - dh dg,这就是李代数上的乘法,记为 [dg,dh]。
这都是不严格的记法。是一种形象化的记忆方法。这个应该是可以严格化的。但是挺费脑筋的。
从这个不严格的记法里看,显然有[dg,dh]=-[dh,dg],也有雅可比规则,[df,[dg,dh]]=[[df,dg],dh]+[dg,[df,dh]]。所以李代数的乘法既是非交换的,也不满足结合律。但是规则性还是很强的。
雅可比规则可以直接从[dg,dh]=dg dh - dh dg中推出。也和求导中的product rule有关。到底哪一个更本质我也没想好。
这些就是李代数的全部定义性质。所以也可以直接代数定义:
李代数就是一个vector space L,其上有一个乘法,记为 [a,b],要求满足:
[a,b]=-[b,a]
[a,[b,c]]=[[a,b],c]+[b,[a,c]]
这个乘法是从李群中导出的。李群一般是非交换群。也就是gh != hg,非交换的程度可以用一个commutator度量,也就是ghg-1h-1,相当于gh/(hg)。李群上的commutator线性化映射到李代数上,相当于变成了减法 dg dh - dh dg。也就是两个tangent vector dg 和 dh,组到一起,dg . dh = dg dh - dh dg,这就是李代数上的乘法,记为 [dg,dh]。
这都是不严格的记法。是一种形象化的记忆方法。这个应该是可以严格化的。但是挺费脑筋的。
从这个不严格的记法里看,显然有[dg,dh]=-[dh,dg],也有雅可比规则,[df,[dg,dh]]=[[df,dg],dh]+[dg,[df,dh]]。所以李代数的乘法既是非交换的,也不满足结合律。但是规则性还是很强的。
雅可比规则可以直接从[dg,dh]=dg dh - dh dg中推出。也和求导中的product rule有关。到底哪一个更本质我也没想好。
这些就是李代数的全部定义性质。所以也可以直接代数定义:
李代数就是一个vector space L,其上有一个乘法,记为 [a,b],要求满足:
[a,b]=-[b,a]
[a,[b,c]]=[[a,b],c]+[b,[a,c]]
x1


上次由 TheMatrix 在 2024年 9月 1日 10:52 修改。
#2 Re: 李代数
[a,b]=-[b,a]说明交换律不成立,但是anti-commutativity成立;
[a,[b,c]]=[[a,b],c]+[b,[a,c]]说明结合律不成立,但是Jacobi identity成立。
还有哪些乘法满足Jacobi identity?它们的共性是什么?有啥用处?
[a,[b,c]]=[[a,b],c]+[b,[a,c]]说明结合律不成立,但是Jacobi identity成立。
还有哪些乘法满足Jacobi identity?它们的共性是什么?有啥用处?
TheMatrix 写了: 2024年 8月 31日 11:14 李代数从李群中来。李群是manifold同时也是一个群。是manifold就有tangent space。李代数是李群在单位元点的tagent space。这个tangent space不仅有vector space结构,还可以定义乘法。
这个乘法是从李群中导出的。李群一般是非交换群。也就是gh != hg,非交换的程度可以用一个commutator度量,也就是ghg-1h-1,相当于gh/(hg)。李群上的commutator线性化映射到李代数上,相当于变成了减法 dg dh - dh dg。也就是两个tangent vector dg 和 dh,组到一起,dg . dh = dg dh - dh dg,这就是李代数上的乘法,记为 [dg,dh]。
这都是不严格的记法。是一种形象化的记忆方法。这个应该是可以严格化的。但是挺费脑筋的。
从这个不严格的记法里看,显然有[dg,dh]=-[dh,dg],也有雅可比规则,[df,[dg,dh]]=[[df,dg],dh]+[dg,[df,dh]]。所以李代数的乘法既是非交换的,也不满足结合律。但是规则性还是很强的。
雅可比规则可以直接从[dg,dh]=dg dh - dh dg中推出。也和求导中的product rule有关。到底哪一个更本质我也没想好。
这些就是李代数的全部定义性质。所以也可以直接代数定义:
李代数就是一个vector space L,其上有一个乘法,记为 [a,b],要求满足:
[a,b]=-[b,a]
[a,[b,c]]=[[a,b],c]+[b,[a,c]]
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13633
- 注册时间: 2022年 7月 26日 00:35
#3 Re: 李代数
有了结构就要定义homomorphism,也就是保持结构的映射。TheMatrix 写了: 2024年 8月 31日 11:14 李代数从李群中来。李群是manifold同时也是一个群。是manifold就有tangent space。李代数是李群在单位元点的tagent space。这个tangent space不仅有vector space结构,还可以定义乘法。
这个乘法是从李群中导出的。李群一般是非交换群。也就是gh != hg,非交换的程度可以用一个commutator度量,也就是ghg-1h-1,相当于gh/(hg)。李群上的commutator线性化映射到李代数上,相当于变成了减法 dg dh - dh dg。也就是两个tangent vector dg 和 dh,组到一起,dg . dh = dg dh - dh dg,这就是李代数上的乘法,记为 [dg,dh]。
这都是不严格的记法。是一种形象化的记忆方法。这个应该是可以严格化的。但是挺费脑筋的。
从这个不严格的记法里看,显然有[dg,dh]=-[dh,dg],也有雅可比规则,[df,[dg,dh]]=[[df,dg],dh]+[dg,[df,dh]]。所以李代数的乘法既是非交换的,也不满足结合律。但是规则性还是很强的。
雅可比规则可以直接从[dg,dh]=dg dh - dh dg中推出。也和求导中的product rule有关。到底哪一个更本质我也没想好。
这些就是李代数的全部定义性质。所以也可以直接代数定义:
李代数就是一个vector space L,其上有一个乘法,记为 [a,b],要求满足:
[a,b]=-[b,a]
[a,[b,c]]=[[a,b],c]+[b,[a,c]]
假设有两个李代数 L 和 M。有一个函数 f: L --> M。保持结构的话,就要求
1,f 是线性变换 - 保持李代数的线性结构。
2,f([a,b])=[f(a),f(b)] - 保持李代数的乘法结构。
这样,f 就是李代数homomorphism。
有了homomorphism就有kernel,也就是 {a∈L: f(a)=0},这是L的一个子集,子空间,子代数,比这些还稍微多一点。有乘法的结构的homomorphism的kernel一般叫ideal,比如环的ideal。
{0}和集合本身是trivial ideal。没有nontrivial ideal的李代数叫 simple 李代数。和单群的定义一样 - 没有能作为kernel的子群的群,叫单群。
由 simple 李代数做direct sum得到的李代数,叫 semisimple 李代数。
还有其他的李代数吗?有。还有 solvable 李代数。以及有 solvable 成分的李代数。
上次由 TheMatrix 在 2024年 8月 31日 15:39 修改。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13633
- 注册时间: 2022年 7月 26日 00:35
#4 Re: 李代数
End(V) 或 matrix 的 symmetric difference乘法,满足雅可比关系:FoxMe 写了: 2024年 8月 31日 11:34 [a,b]=-[b,a]说明交换律不成立,但是anti-commutativity成立;
[a,[b,c]]=[[a,b],c]+[b,[a,c]]说明结合律不成立,但是Jacobi identity成立。
还有哪些乘法满足Jacobi identity?它们的共性是什么?有啥用处?
[A,B]=AB-BA,那么 [A,[B,C]]=[[A,B],C]+[B,[A,C]]
derivation和雅可比关系形似:d(f.g) = df.g+f.dg。
如果d和f和g在同一个空间里的话,就成了雅可比关系。
所以雅可比关系应该和两个东西有关系:
1, symmetric difference
2, derivation
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13633
- 注册时间: 2022年 7月 26日 00:35
#5 Re: 李代数
direct sum在任何结构中都存在。假设A和B是一个结构中的两个物体,A⊕B就是A和B完全独立,各自变化。TheMatrix 写了: 2024年 8月 31日 11:43 有了结构就要定义homomorphism,也就是保持结构的映射。
假设有两个李代数 L 和 M。有一个函数 f: L --> M。保持结构的话,就要求
1,f 是线性变换 - 保持李代数的线性结构。
2,f([a,b])=[f(a),f(b)] - 保持李代数的乘法结构。
这样,f 就是李代数homomorphism。
有了homomorphism就有kernel,也就是 {a∈L: f(a)=0},这是L的一个子集,子空间,子代数,比这些还稍微多一点。有乘法的结构的homomorphism的kernel一般叫ideal,比如环的ideal。
{0}和集合本身是trivial ideal,没有nontrivial ideal的李代数叫 simple 李代数。和单群的定义一样 - 没有能作为kernel的子群的群,叫单群。
由 simple 李代数做direct sum得到的李代数,叫 semisimple 李代数。
还有其他的李代数吗?有。还有 solvable 李代数。以及有 solvable 成分的李代数。
solvable 李代数是
L(0) = L
L(1) = [L,L] := {[a,b] for all a,b∈L}
L(2) = [L(1),L(1)]
...
eventually, L(n)={0}。
这是一个tower of ideal,一个套一个的ideal tower。所以它不是simple 李代数,而它又不能写成direct sum。
好像所有有乘法结构的代数,都有这个情况。就是除了simple和semisimple之外还有别的情况。
上次由 TheMatrix 在 2024年 8月 31日 15:41 修改。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13633
- 注册时间: 2022年 7月 26日 00:35
#6 Re: 李代数
homomorphism也告诉了什么是isomorphism。TheMatrix 写了: 2024年 8月 31日 11:43 有了结构就要定义homomorphism,也就是保持结构的映射。
假设有两个李代数 L 和 M。有一个函数 f: L --> M。保持结构的话,就要求
1,f 是线性变换 - 保持李代数的线性结构。
2,f([a,b])=[f(a),f(b)] - 保持李代数的乘法结构。
这样,f 就是李代数homomorphism。
有了homomorphism就有kernel,也就是 {a∈L: f(a)=0},这是L的一个子集,子空间,子代数,比这些还稍微多一点。有乘法的结构的homomorphism的kernel一般叫ideal,比如环的ideal。
{0}和集合本身是trivial ideal,没有nontrivial ideal的李代数叫 simple 李代数。和单群的定义一样 - 没有能作为kernel的子群的群,叫单群。
由 simple 李代数做direct sum得到的李代数,叫 semisimple 李代数。
还有其他的李代数吗?有。还有 solvable 李代数。以及有 solvable 成分的李代数。
如果有双向的homomorphism,f: L --> M, g: M --> L, 而且f∘g和g∘f是各自空间上的identity映射,那么f和g是L和M之间的isomorphism。也就是L和M是disguised same thing。元素之间only different by labeling。
这很重要:这样在一个概念中,谁是谁,谁不是谁,就清楚了。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13633
- 注册时间: 2022年 7月 26日 00:35
#7 Re: 李代数
simple 李代数的分类已经完成,是借助李代数的表示论完成的。主要是Cartan的贡献。TheMatrix 写了: 2024年 8月 31日 11:43 有了结构就要定义homomorphism,也就是保持结构的映射。
假设有两个李代数 L 和 M。有一个函数 f: L --> M。保持结构的话,就要求
1,f 是线性变换 - 保持李代数的线性结构。
2,f([a,b])=[f(a),f(b)] - 保持李代数的乘法结构。
这样,f 就是李代数homomorphism。
有了homomorphism就有kernel,也就是 {a∈L: f(a)=0},这是L的一个子集,子空间,子代数,比这些还稍微多一点。有乘法的结构的homomorphism的kernel一般叫ideal,比如环的ideal。
{0}和集合本身是trivial ideal,没有nontrivial ideal的李代数叫 simple 李代数。和单群的定义一样 - 没有能作为kernel的子群的群,叫单群。
由 simple 李代数做direct sum得到的李代数,叫 semisimple 李代数。
还有其他的李代数吗?有。还有 solvable 李代数。以及有 solvable 成分的李代数。
李代数也有表示论。可以从李群的表示论中导出。也可以直接定义。
ρ: L --> End(V)
就是李代数 L 在线性空间V上的表示。这是一个李代数 L 到李代数 End(V) 之间的homomorphism。
End(V)是V上的线性变换构成的空间:{f: V --> V}。这也是一个李代数:A,B∈End(V),乘法定义为[A,B]=AB-BA。
所以End(V)上有两个乘法,AB,这是matrix乘法。[A,B],这是symmetric difference乘法。所以End(V)上有两个代数结构,一个是matrix algebra,一个是李代数的algebra。
从action来看,一个X∈L,作用在v∈V上,记为X.v,它等于ρ(X)(v),也就是ρ(X)这个matrix作用在v上。
那么 [X,Y].v = X.Y.v - Y.X.v,李代数L这边的乘法,到了matrix这边成了symmetric difference乘法,也是End(V)作为李代数的乘法。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13633
- 注册时间: 2022年 7月 26日 00:35
#8 Re: 李代数
李代数的表示论怎么再往下走一步呢?有限群的表示论很难借鉴了,因为李群是连续群,很无限。TheMatrix 写了: 2024年 8月 31日 12:51 simple 李代数的分类已经完成,是借助李代数的表示论完成的。主要是Cartan的贡献。
李代数也有表示论。可以从李群的表示论中导出。也可以直接定义。
ρ: L --> End(V)
就是李代数 L 在线性空间V上的表示。这是一个李代数 L 到李代数 End(V) 之间的homomorphism。
End(V)是V上的线性变换构成的空间:{f: V --> V}。这也是一个李代数:A,B∈End(V),乘法定义为[A,B]=AB-BA。
所以End(V)上有两个乘法,AB,这是matrix乘法。[A,B],这是symmetric difference乘法。所以End(V)上有两个代数结构,一个是matrix algebra,一个是李代数的algebra。
从action来看,一个X∈L,作用在v∈V上,记为X.v,它等于ρ(X)(v),也就是ρ(X)这个matrix作用在v上。
那么 [X,Y].v = X.Y.v - Y.X.v,李代数L这边的乘法,到了matrix这边成了symmetric difference乘法,也是End(V)作为李代数的乘法。
Cartan subalgebra横空出世。
假设L是一个李代数,simple 李代数。Cartan subalgebra,H,是L里面的一个子代数,maximal abelian subalgebra。
首先 L 是simple 李代数,它里面没有ideal,但是可以有子代数,subalgebra。也就是这个子代数对乘法封闭就行。就好像单群里没有正规子群,但是可以有子群一样。
abelian是可交换,也就是[X,Y]=0,因为[X,Y]=XY-YX,[X,Y]=0就是XY=YX。这要在matrix的表示中make sense。
还要maximal,也就是最大的这样的子代数。最大的意思是,在一条一个套一个的子代数的tower的线索的顶点上。在这条线索上没有比它更大的,就是最大的。最大的可以不唯一。每一条线索上有一个最大的。
maximal通常可以作为一个物体的特征,因为一个物体中从某方面看只有一个maximal的子结构。不同物体从它们各自的maximal子结构看应该也不同 - 如果相同那就说它们在这个角度上归为同一类。这是哲学,或者语言学上的意义。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13633
- 注册时间: 2022年 7月 26日 00:35
#9 Re: 李代数
为什么要abelian呢?因为abelian的话,变成matrix之后乘法可交换,那么可以同时对角化,simultaneously diagonalizable。TheMatrix 写了: 2024年 8月 31日 13:40 李代数的表示论怎么再往下走一步呢?有限群的表示论很难借鉴了,因为李群是连续群,很无限。
Cartan subalgebra横空出世。
假设L是一个李代数,simple 李代数。Cartan subalgebra,H,是L里面的一个子代数,maximal abelian subalgebra。
首先 L 是simple 李代数,它里面没有ideal,但是可以有子代数,subalgebra。也就是这个子代数对乘法封闭就行。就好像单群里没有正规子群,但是可以有子群一样。
abelian是可交换,也就是[X,Y]=0,因为[X,Y]=XY-YX,[X,Y]=0就是XY=YX。这要在matrix的表示中make sense。
还要maximal,也就是最大的这样的子代数。最大的意思是,在一条一个套一个的子代数的tower的线索的顶点上。在这条线索上没有比它更大的,就是最大的。最大的可以不唯一。每一条线索上有一个最大的。
maximal通常可以作为一个物体的特征,因为一个物体中从某方面看只有一个maximal的子结构。不同物体从它们各自的maximal子结构看应该也不同 - 如果相同那就说它们在这个角度上归为同一类。这是哲学,或者语言学上的意义。
为什么要同时对角化呢?
过程应该是这样的:最开始随便拿一个X∈L,在一个表示中,变成matrix之后,它可以对角化,(以复数为系数的话,所有matrix都可以对角化)。对角线上都是eigenvalue。
“取”一个eigenvalue,λ,赋值给这个X,这就变成了X到λ的映射。每一个X都有一个λ,定义了L上的一个函数,一个数值函数,也叫一个functional。总共有n个eigenvalue的话,就有了n个functional。然后研究n个functional之间的关系,希望能得出点结论。
但是这个过程有几个问题。
首先“取”一个eigenvalue - 你不知道取哪个,eigenvalue有n个,但是没有标记,没有顺序。但是eigenvalue可以以eigenvector为标记。以eigenvector为标记的话,X的eigenvector和Y的eigenvector必须一样。这样有n个eigenvector,对应的每一个X或Y就有相应的eigenvalue。这就要求X和Y有common eigenvector。
而有common eigenvector这个要求是不能扩大到全部李代数L上的。而在abelian子代数上,所有元素能同时对角化,也就是有common eigenvector。
所以functional这个思路,只能在abelian subalgebra上实施。再加上前面对maximal的阐述,就变成了maximal abelian subalgebra,也就是Cartan subalgebra。
整个这个过程中,好多东西要互相合拍。这是一种安排,人为的安排,不是说必然会出现什么。这就是发明。所以叫横空出世。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13633
- 注册时间: 2022年 7月 26日 00:35
#10 Re: 李代数
还有一个就是,Cartan那个时候的人,应该对matrix很熟。一个matrix Lie algebra中,maximal abelian subalgebra什么样,应该都是很熟悉的。TheMatrix 写了: 2024年 8月 31日 14:06 为什么要abelian呢?因为abelian的话,变成matrix之后乘法可交换,那么可以同时对角化,simultaneously diagonalizable。
为什么要同时对角化呢?
过程应该是这样的:最开始随便拿一个X∈L,在一个表示中,变成matrix之后,它可以对角化,(以复数为系数的话,所有matrix都可以对角化)。对角线上都是eigenvalue。
“取”一个eigenvalue,λ,赋值给这个X,这就变成了X到λ的映射。每一个X都有一个λ,定义了L上的一个函数,一个数值函数,也叫一个functional。总共有n个eigenvalue的话,就有了n个functional。然后研究n个functional之间的关系,希望能得出点结论。
但是这个过程有几个问题。
首先“取”一个eigenvalue - 你不知道取哪个,eigenvalue有n个,但是没有标记,没有顺序。但是eigenvalue可以以eigenvector为标记。以eigenvector为标记的话,X的eigenvector和Y的eigenvector必须一样。这样有n个eigenvector,对应的每一个X或Y就有相应的eigenvalue。这就要求X和Y有common eigenvector。
而有common eigenvector这个要求是不能扩大到全部李代数L上的。而在abelian子代数上,所有元素能同时对角化,也就是有common eigenvector。
所以functional这个思路,只能在abelian subalgebra上实施。再加上前面对maximal的阐述,就变成了maximal abelian subalgebra,也就是Cartan subalgebra。
整个这个过程中,好多东西要互相合拍。这是一种安排,人为的安排,不是说必然会出现什么。这就是发明。所以叫横空出世。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13633
- 注册时间: 2022年 7月 26日 00:35
#11 Re: 李代数
另一方面,是发明的话,就也可以不这么发明,可以有其他的路走。TheMatrix 写了: 2024年 8月 31日 14:06 为什么要abelian呢?因为abelian的话,变成matrix之后乘法可交换,那么可以同时对角化,simultaneously diagonalizable。
为什么要同时对角化呢?
过程应该是这样的:最开始随便拿一个X∈L,在一个表示中,变成matrix之后,它可以对角化,(以复数为系数的话,所有matrix都可以对角化)。对角线上都是eigenvalue。
“取”一个eigenvalue,λ,赋值给这个X,这就变成了X到λ的映射。每一个X都有一个λ,定义了L上的一个函数,一个数值函数,也叫一个functional。总共有n个eigenvalue的话,就有了n个functional。然后研究n个functional之间的关系,希望能得出点结论。
但是这个过程有几个问题。
首先“取”一个eigenvalue - 你不知道取哪个,eigenvalue有n个,但是没有标记,没有顺序。但是eigenvalue可以以eigenvector为标记。以eigenvector为标记的话,X的eigenvector和Y的eigenvector必须一样。这样有n个eigenvector,对应的每一个X或Y就有相应的eigenvalue。这就要求X和Y有common eigenvector。
而有common eigenvector这个要求是不能扩大到全部李代数L上的。而在abelian子代数上,所有元素能同时对角化,也就是有common eigenvector。
所以functional这个思路,只能在abelian subalgebra上实施。再加上前面对maximal的阐述,就变成了maximal abelian subalgebra,也就是Cartan subalgebra。
整个这个过程中,好多东西要互相合拍。这是一种安排,人为的安排,不是说必然会出现什么。这就是发明。所以叫横空出世。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13633
- 注册时间: 2022年 7月 26日 00:35
#12 Re: 李代数
所以按照这条路走,就有一个李代数 L,假设为simple,有一个Cartan subalgebra H ⊆ L。TheMatrix 写了: 2024年 8月 31日 14:06 为什么要abelian呢?因为abelian的话,变成matrix之后乘法可交换,那么可以同时对角化,simultaneously diagonalizable。
为什么要同时对角化呢?
过程应该是这样的:最开始随便拿一个X∈L,在一个表示中,变成matrix之后,它可以对角化,(以复数为系数的话,所有matrix都可以对角化)。对角线上都是eigenvalue。
“取”一个eigenvalue,λ,赋值给这个X,这就变成了X到λ的映射。每一个X都有一个λ,定义了L上的一个函数,一个数值函数,也叫一个functional。总共有n个eigenvalue的话,就有了n个functional。然后研究n个functional之间的关系,希望能得出点结论。
但是这个过程有几个问题。
首先“取”一个eigenvalue - 你不知道取哪个,eigenvalue有n个,但是没有标记,没有顺序。但是eigenvalue可以以eigenvector为标记。以eigenvector为标记的话,X的eigenvector和Y的eigenvector必须一样。这样有n个eigenvector,对应的每一个X或Y就有相应的eigenvalue。这就要求X和Y有common eigenvector。
而有common eigenvector这个要求是不能扩大到全部李代数L上的。而在abelian子代数上,所有元素能同时对角化,也就是有common eigenvector。
所以functional这个思路,只能在abelian subalgebra上实施。再加上前面对maximal的阐述,就变成了maximal abelian subalgebra,也就是Cartan subalgebra。
整个这个过程中,好多东西要互相合拍。这是一种安排,人为的安排,不是说必然会出现什么。这就是发明。所以叫横空出世。
有一个李代数的表示,V,也就是 ρ: L --> End(V)。
假设V有n维,L有m维,H有h维。h ≤ m。
对于H来说,V会裂解为n个eigenvector,它们是H上所有元素的common eigenvector。每一个eigenvector都label了一个H上的,注意不是L上的,functional,是对应的eigenvalue。
总共有n个这样的functional。这n个functional,叫weight。实际上就是eigenvalue。
而H只有h维,如果 n > h 的话,那么这n个functional不全都线性无关。
这是一般的V。而李代数L本身也是一个线性空间,也有一个L的表示 - 任何一个代数上,乘法都可以看成自身的一个线性变换,也就是自己在自己上的一个表示。李代数中,这个表示叫adjoint representation。也就是 adj: L --> End(L)。它也有weight,称为root。
总共有m个root,在h维线性空间中,m是L的维度,h是H的维度。h ≤ m,所以这m个root一定线性相关。其中只有h个是线性无关的,它们也是这h维functional空间的基,叫simple root。
但是它们不是正交基,有一种方法可以定义它们之间的内积。组合起来形成一个 h * h 的matrix,叫Cartan matrix。可见Cartan已经把这些root放到欧几里得空间中看它们的位置关系了。这些root以及它们之间的位置关系,叫root system。
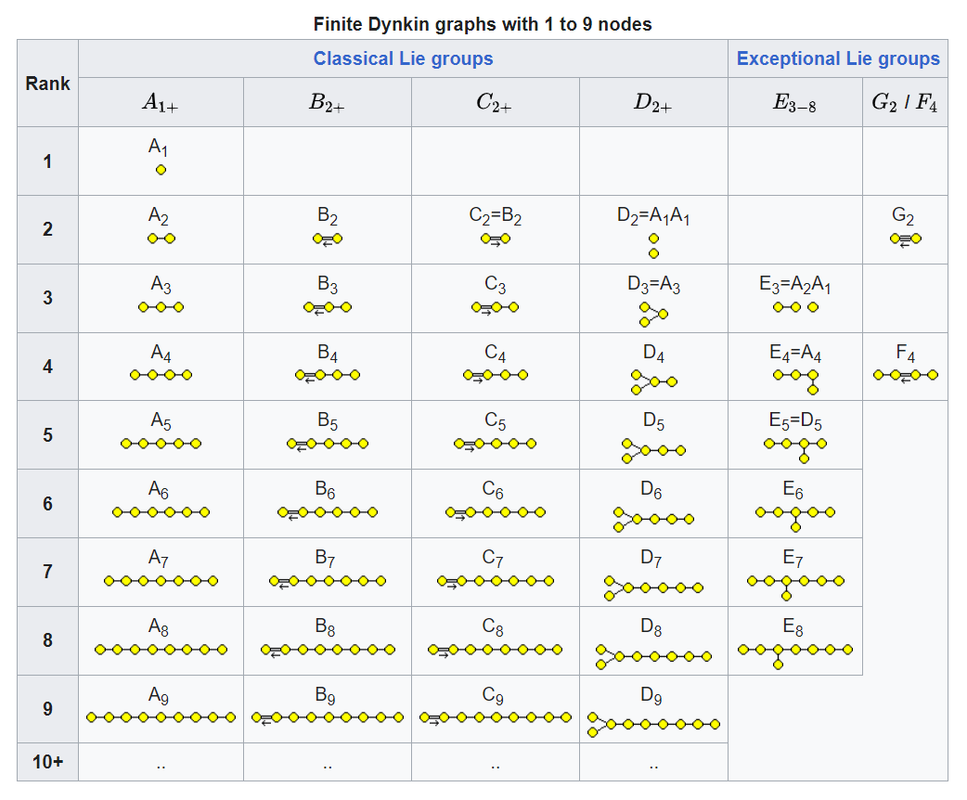
root system上的位置关系是非常restrictive的。两个simple root之间只有几个可能的夹角,以及长度的比例,再加上总的个数。所以root system的形态可以完全分类。这就是simple Lie algebra的完全分类。又叫Dynkin diagram。
总共有9类:
Classical 有4类:An, Bn, Cn, Dn。
Exceptional 有5类:E6, E7, E8, G2, F4。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13633
- 注册时间: 2022年 7月 26日 00:35
#14 Re: 李代数
我也一直没搞懂。最近看了一下,好像是这么回事:
一个semisimple李代数 L,它有一个root system,也就是全部root的位置关系。
一个root是Cartan subalgebra H上的一个functional。比如λ是一个root的话,那么for X ∈ H,λ(X)是X的adjoint representation的eigenvalue。
L有n维的话,那么总共有n个root。每一个root对应一个eigenvector。
而H是Cartan subalgebra,它只有h维,h ≤ n,所以H上的functional只能有h个线性无关的,也就是只能有h个root是独立的,这叫simple root。
simple root之间有inner product,也就是它们存在于欧几里得空间之中。也就有位置关系。长度,角度。
simple root之间inner product有非常强的限制。只能取四个数,0,1,2,3。这个怎么算出来的呢?我也没仔细看。
所以两个simple root之间的夹角,只能有4个值:90°,120°,135°,150°。对应长度之比也是固定的。90°的叫orthogonal,长度之比没有要求。120°的两个root长度必须相等,135°的两个root长度之比为√2,150°的两个root长度之比为√3。
Dynkin diagram是以点线来表示simple root之间位置关系的图:一个simple root是一个点。夹角为90°的两个simple root之间为orthogonal,没有连线。夹角为120°的两个simple root之间有单线连接,夹角为135°的有双线连接,夹角为150°的有三线连接。连线上还可以画上箭头,长度大的simple root指向长度小的simple root。这就是Dynkin diagram.
Dynkin diagram可以用来fully classify simple Lie algebra。
比如Dynkin diagram只有两个点的,总共可以有多少种不同的图?有限的。三个点的呢?也是有限的。就这样往上走,就发现只有9种不同的Dynkin diagram。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13633
- 注册时间: 2022年 7月 26日 00:35
#16 Re: 李代数
比如Bn root system。TheMatrix 写了: 2024年 8月 31日 15:11
总共有9类:
Classical 有4类:An, Bn, Cn, Dn。
Exceptional 有5类:E6, E7, E8, G2, F4。

它代表so2n+1,odd orthogonal Lie algebra。
n是Cartan subalgebra的维度,也叫rank。
Lie algebra本身的维度是n(2n+1)。
Cartan subalgebra作用在Lie algebra上,作用在自己的部分等于0,因为这是adjoint action。作用在其余的部分有eigenvector,共n(2n+1)-n=2n2。所以一共有2n2个root。但是它们所在的空间只有n维,等于Cartan subalgebra的维度。所以其中只有n个线性无关的,叫simple root。
比如B3。它代表so(7)。so(7)本身的维度是3*7=21维。减去Cartan subalgebra的维度就是18,所以总共有18个root,其中只有n=3个simple root。也就是18个root在3维空间中。
Dynkin diagram有3个node,代表3个simple root。从左到右是X,Y,Z:
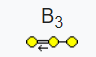
simple root之间都取钝角。X和Y之间是双线,代表夹角为135°,也代表root长度比例是√2。双线上的箭头代表Y比X的长度大。Y和Z之间是单线,代表夹角为120°,也代表长度相等。X和Z之间没有连接,代表orthogonal。其余的root都是由这三个simple root做integer linear combination生成。而且integer只能取0,1,-1。
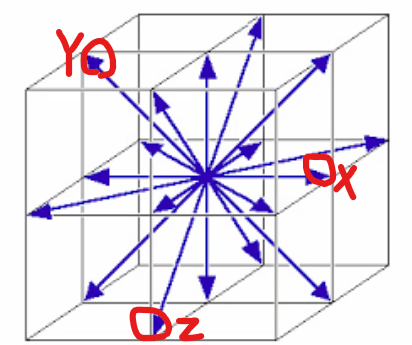
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13633
- 注册时间: 2022年 7月 26日 00:35
#17 Re: 李代数
这个好像不对。我看到一个root等于2X+Y+Z。TheMatrix 写了: 2024年 9月 2日 11:05 其余的root都是由这三个simple root做integer linear combination生成。而且integer只能取0,1,-1。
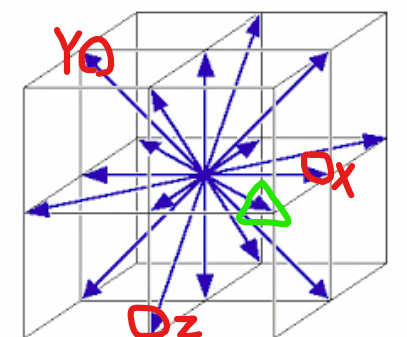
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13633
- 注册时间: 2022年 7月 26日 00:35
#18 Re: 李代数
嗯。确实。Cartan subalgebra就是最大对易算符集合。物理意义就是能同时确定的observable。确实是物理学家发明的。也谈不上发明了,大家很自然就提出这个概念了。verdelite 写了: 2024年 8月 31日 20:32 谈不上横空出世吧。看着是先有量子力学,后有李代数。量子力学里面的泊松括号表示法,看着和这个李代数的东西差不多。看起来又是数学家把物理学家的数学规范化了。
任何一个observable,就是这里的李代数里的一个元素X,也是一个operator,都有n个eigenvalue和eigenvector。如果其中一个是X.v=λv。那么其他的可以根据这个,在几个方向上做加减得到:
假设包含X的最大对易集合是H,也就是Cartan subalgebra。假设simple root是a,b,c,对应simple root vector是A,B,C,也就是[X,A]=aA,那么X.(Av)=(λ+a)Av,也就是Av也是X的eigenvector,对应新的eigenvalue λ+a。
#19 Re: 李代数
噢,多想介绍。
TheMatrix 写了: 2024年 9月 2日 11:05 比如Bn root system。
它代表so2n+1,odd orthogonal Lie algebra。
n是Cartan subalgebra的维度,也叫rank。
Lie algebra本身的维度是n(2n+1)。
Cartan subalgebra作用在Lie algebra上,作用在自己的部分等于0,因为这是adjoint action。作用在其余的部分有eigenvector,共n(2n+1)-n=2n2。所以一共有2n2个root。但是它们所在的空间只有n维,等于Cartan subalgebra的维度。所以其中只有n个线性无关的,叫simple root。
比如B3。它代表so(7)。so(7)本身的维度是3*7=21维。减去Cartan subalgebra的维度就是18,所以总共有18个root,其中只有n=3个simple root。也就是18个root在3维空间中。
Dynkin diagram有3个node,代表3个simple root。从左到右是X,Y,Z:
simple root之间都取钝角。X和Y之间是双线,代表夹角为135°,也代表root长度比例是√2。双线上的箭头代表Y比X的长度大。Y和Z之间是单线,代表夹角为120°,也代表长度相等。X和Z之间没有连接,代表orthogonal。其余的root都是由这三个simple root做integer linear combination生成。而且integer只能取0,1,-1。


