我给你看一下copilot屎一样的表现
版主: 牛河梁
#1 我给你看一下copilot屎一样的表现
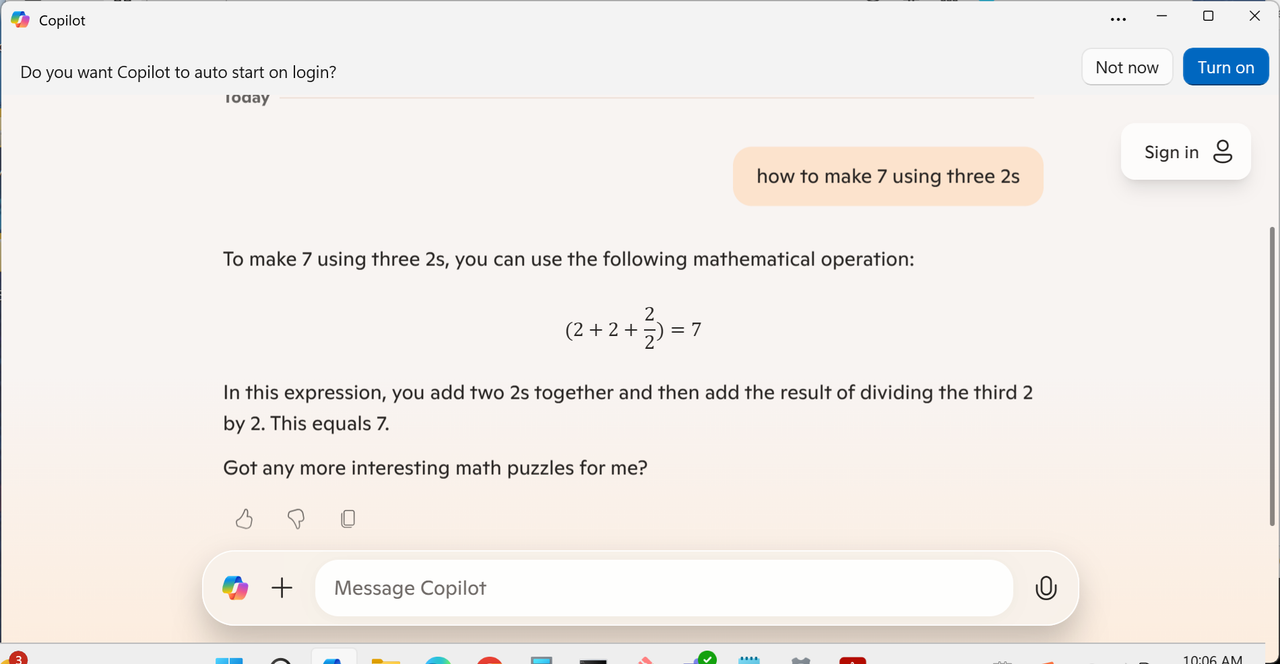
how to to make 7 with 3 2s
这是他给出的答案,还tmd拒不认错
(2x2)+(2/2)+2= 4+1+2=7
这是他给出的答案,还tmd拒不认错
(2x2)+(2/2)+2= 4+1+2=7
If printing money would end poverty, printing diplomas would end stupidity.
#3 Re: 我给你看一下copilot屎一样的表现
我老说this is not correct,丫的回答
I apologize for that mistake. Let's try another approach to make 7 using three 2s:
$$ 2 + 2 + (2 / 2) = 2 + 2 + 1 = 5 $$
Hmm, that doesn't work either. Let's try again:
$$ 2 \times 2 + 2 + (2 / 2) = 4 + 2 + 1 = 7 $$
This should be correct. Thank you for your patience! Would you like to explore more math puzzles or anything else?
这就这个表现还和别人比个p啊
I apologize for that mistake. Let's try another approach to make 7 using three 2s:
$$ 2 + 2 + (2 / 2) = 2 + 2 + 1 = 5 $$
Hmm, that doesn't work either. Let's try again:
$$ 2 \times 2 + 2 + (2 / 2) = 4 + 2 + 1 = 7 $$
This should be correct. Thank you for your patience! Would you like to explore more math puzzles or anything else?
这就这个表现还和别人比个p啊
If printing money would end poverty, printing diplomas would end stupidity.
#4 Re: 我给你看一下copilot屎一样的表现
哈哈哈哈,好吧,难怪你软啥新项目干的跟狗屎一样
If printing money would end poverty, printing diplomas would end stupidity.
#5 Re: 我给你看一下copilot屎一样的表现
x2


上次由 biggestballs 在 2025年 2月 23日 10:09 修改。
Devil doesn't need an advocate
#6 Re: 我给你看一下copilot屎一样的表现
lol,您这是转圈给你软丢人啊
If printing money would end poverty, printing diplomas would end stupidity.
#7 Re: 我给你看一下copilot屎一样的表现
我好心提示你,登录你的gpt账号。目前我只看到o3-high打开搜索时候能给出相对最elegant的结果
If printing money would end poverty, printing diplomas would end stupidity.
#8 Re: 我给你看一下copilot屎一样的表现
丢你M的人啊,你给我找个不同答案出来
尼玛/2跟*2中的这两个2根本不能算在三个2里面,不然根本做不到
尼玛/2跟*2中的这两个2根本不能算在三个2里面,不然根本做不到
上次由 biggestballs 在 2025年 2月 23日 10:11 修改。
Devil doesn't need an advocate
#11 Re: 我给你看一下copilot屎一样的表现
看到你的表现,我觉得你软的确可以用ai把马工都取代了。都是不识数啊
给你看看deepshit的表现
Okay, so I need to figure out how to make the number 7 using only three 2s. Hmm, let's see. The problem says "using only 3 2s," so I can use the digits 2, 2, and 2, and combine them with mathematical operations. Alright, let's start thinking about different operations I can use.
First, the basic ones: addition, subtraction, multiplication, division. Maybe exponents or factorials? The problem doesn't specify any restrictions, so I guess those are allowed. Let me try combining them step by step.
If I just add them all together: 2 + 2 + 2 = 6. That's too low. Not enough. What if I multiply some and add? Like 2 * 2 + 2 = 4 + 2 = 6. Still 6. Hmm. Maybe subtract instead? 2 * 2 - 2 = 4 - 2 = 2. Nope, that's worse. What if I use division? Let's see. 2 + 2 + (2/2) would use a fourth 2, which I don't have. Wait, no, I can only use three 2s. So division might not help here unless I structure it differently.
Wait, maybe exponents. Let's try that. 2^2 + 2 = 4 + 2 = 6. Still 6. How about 2^(2 + 2) = 2^4 = 16. That's way too high. Maybe 2^3, but I don't have a 3. Wait, can I use the number 3? No, only 2s. So exponents, but how? Let me think. If I use 2 squared plus 2, but that's the same as before.
Factorials? 2! is 2. So 2! + 2! + 2! = 6. Still 6. If I do (2 + 2)! + 2 = 24 + 2 = 26. That's way too big. Maybe 2 + 2 + 2! = 2 + 2 + 2 = 6. Still same result. Hmm.
What if I use decimal points? Like 2.2 or something? The problem didn't specify if decimal points are allowed. If they are, maybe 2.2 + 2.2 + 2.2 = 6.6. Not 7. Close, but not quite. Alternatively, combining numbers. For example, 22 divided by 2. Let's see: 22 / 2 = 11. That's too high. How about 2/2 + 2 = 1 + 2 = 3. Still low.
Wait, maybe concatenation is allowed. Like putting two 2s together to make 22. If so, then maybe 22 divided by 2 minus something. Wait, 22 divided by 2 is 11. If I subtract 2, that's 9. If I add 2 instead, that's 13. Not helpful. Alternatively, 2 + 2 + 2 = 6. Hmm. What if I use square roots? Sqrt(2) is approximately 1.414. So sqrt(2) + sqrt(2) + 2. But that would be roughly 1.414 + 1.414 + 2 = 4.828. Still not 7. And also, does the problem allow square roots? It might be stretching the rules.
Wait, maybe using exponents and factorials together. Let's think. For example, 2^(2) + 2! = 4 + 2 = 6. Still 6. How about (2 + 2)! / 2 = 24 / 2 = 12. Still not 7. Hmm.
What if I use decimal fractions with exponents? Like 2^(2) + 2.2? But that would be 4 + 2.2 = 6.2. Still not 7. Maybe 2.2 * 2 + 2? That would be 4.4 + 2 = 6.4. Closer, but not there yet.
Wait, maybe combining operations in a different order. For example, 2 + (2 * 2) = 2 + 4 = 6. Nope. What if I do 2 * 2 * 2 = 8. Oh, that's 8. Close to 7. How can I subtract 1 from 8? But how do I get 1 from a 2? Wait, 2/2 is 1. But then I would need a fourth 2. Let's see: 2 * 2 * 2 - (2/2). But that's four 2s. Not allowed. So that's out.
Alternatively, maybe 2^3 - something, but again, 3 isn't allowed. Unless I can make 3 from two 2s. 2 + 2/2 = 3. But that uses three 2s. So then 2^(2 + 2/2) = 2^3 = 8. Then subtract 1? But again, how to get 1. Wait, this is getting complicated.
Wait, maybe using a different approach. Let's see. If I can use decimal points, maybe 2.2 + 2.2 + 2.2 = 6.6. Not 7. If I can concatenate two 2s into 22, then 22 divided by something. 22 - 2 = 20. 22 / 2 = 11. 22 + 2 = 24. Not helpful.
Wait, what if I use exponents with decimals. Like 2^(3) - 1 = 8 -1 =7. But how to get 3 and 1 from 2s. Alternatively, 2 squared plus 2 squared minus 1. But again, getting 1 from a 2. Maybe 2/2. But again, that would require extra 2s.
Hold on, maybe using factorial and division. Let's think. For example, (2 + 2)! / 2 - 2. But that would be 24 / 2 - 2 = 12 - 2 = 10. Still not 7. Alternatively, (2! + 2! + 2!) = 6. No.
Wait, here's an idea. If I take 2 and do a factorial, that's 2. Then another factorial? 2!! which is 2. Doesn't help. Wait, maybe 2 + 2 = 4, and then 4! is 24. 24 divided by 2 is 12. Still not 7. Hmm.
Wait, let's think outside the box. Maybe using square roots and exponents. For example, sqrt(2) is about 1.414. So sqrt(2) * sqrt(2) = 2. But that's just back to 2. Hmm.
What if I do something like 2^2 + 2 + 2. But that's four 2s. Wait, no. If I can use three 2s, let's see. Wait, 2 squared is 4, plus 2 plus 2 is 8. But that's four 2s again.
Wait, maybe using decimal fractions in a different way. For example, .2 as 0.2. But the problem says "using only 3 2s", so can I use a decimal like .2? That might count as using a 2. So maybe 2 + 2 + 2. But that's 6. Wait, 2 / .2 = 10. If I do 2 / .2 + 2, that would be 10 + 2 = 12. But that uses two 2s for the 0.2 and one more 2. So total three 2s? Wait, .2 is just one 2. So 2 / 0.2 is 10, using one 2 for the numerator and one for the decimal. Then adding another 2. So total three 2s: 2 / .2 + 2. Let me check that. Yes: 2 divided by 0.2 is 10, plus 2 is 12. But we need 7. Hmm. Not helpful.
Wait, maybe 2 + 2 / .2. That's 2 + 10 = 12. Still not 7. Alternatively, 2 * 2 / .2. That's 4 / 0.2 = 20. No.
Alternatively, if I use a repeating decimal? Like .2 repeating? But that might be more complicated and not sure if allowed.
Wait, what if I use exponents with decimals? For example, (2 + 2)^2 = 16. But that's four 2s. Wait, 2 + 2 is two 2s, then squared is another operation. Hmm, not sure.
Wait, here's another idea. Using logarithms? But that seems complicated and probably not allowed. For example, log base 2 of something. But that might be stretching the rules.
Alternatively, using square roots in exponents. For example, 2^(sqrt(2)) is roughly 2.665. But adding those up? Not helpful.
Wait, perhaps using subtraction and division. Let's see. For example, (2 * 2) - (2 / 2) = 4 - 1 = 3. But again, that uses four 2s. No.
Wait, maybe 2^2 + 2 + 2, but that's four 2s. Not allowed.
Hold on, maybe using a combination of operations with different precedences. For example, 2 + 2 + 2 = 6. Not enough. 2 * 2 + 2 = 6. Still no. 2 + 2 * 2 = 6. Hmm.
Wait, what if I use fractions. Like 2 + 2 + 2/2. But that's four 2s. So no. Alternatively, 22/2 - something. 22/2 is 11. 11 - 2 = 9. 11 - (2+2) = 7. Wait, 11 - (2+2) is 7. But that would be 22/2 - (2+2) = 11 - 4 = 7. Let's count the 2s: 22 uses two 2s, divided by 2 is another 2, so that's three 2s. Then subtracting (2+2) would be two more 2s. So total five 2s. No, that's way over. So that's not allowed.
Wait, maybe there's a different way to arrange them. Let's see. How about 2 + 2 + 2 = 6. Then, is there a way to turn that 6 into 7 with the same three 2s? Maybe not.
Wait, another thought: Using decimal concatenation. For instance, 2.2 + 2.2 + 2.6, but we can't make 2.6. Alternatively, 2.2 + 2.8, but again, how to get 2.8 with a 2. Maybe 2.2 + 2.2 + 2.2 = 6.6. Still not 7.
Wait, maybe using percentages? 2% as 0.02. But that seems too small. 2 + 2 + 2% = 4.02. Not helpful.
Alternatively, using 2 in different number bases. For example, if we interpret the numbers in base 3 or something. But the problem doesn't specify. That might be cheating.
Wait, here's a different approach. What if we use the factorial of a decimal? For example, (2 + 2/2)! = (2 +1)! = 3! = 6. But again, 6. And that uses three 2s: 2, 2/2. Wait, 2 + (2/2) = 3. Then 3! =6. So total three 2s. But that gives us 6, not 7. Hmm.
Wait, what about using a repeating decimal? Like 2.\overline{2} which is 2.222... But that's approximately 2.222, and adding another 2 would be 2.222 + 2 + 2 = 6.222. Not 7.
Alternatively, combining 2s with other mathematical symbols. Maybe square root symbols without numbers. Wait, but square root of what? If I take the square root of 2, that's still a 2 inside. So sqrt(2) + sqrt(2) + 2 is approximately 1.414 +1.414 +2 = 4.828. Not enough.
Wait, perhaps using the gamma function, which extends factorials. Gamma(3) = 2! = 2. But not helpful. Gamma(4) = 6. Still 6.
Hmm, this is getting frustrating. Let me think again. The key is to use exactly three 2s with any operations. Maybe there's a trick here. Let's check if someone else has encountered this before. Wait, I recall that sometimes people use the notation where they put a bar over a number to indicate repeating decimals, but does that help here? For example, .2 with a bar over it is 0.222..., which is 2/9. Then 2 / (2/9) = 9. But that uses two 2s. Then 9 - 2 = 7. So total three 2s: 2 / (.\overline{2}) - 2. Let's check: .\overline{2} is 2/9, so 2 divided by (2/9) is 9, then subtract 2 gives 7. But does the notation .\overline{2} count as using a single 2? Because the bar is an operator, not a digit. So maybe that's acceptable. So 2 / 0.\overline{2} - 2 = 9 -2 =7. Let's count the 2s: the 2 in the numerator, the 2 in the repeating decimal, and the 2 being subtracted. So three 2s. That might work. But is this a standard notation? The problem didn't specify whether repeating decimals are allowed, but if they are, this could be a solution.
Alternatively, using the decimal point and a bar for repeating, which is a common mathematical notation. So 0.\overline{2} is 0.222..., which is 2/9. Therefore, the calculation would be 2 divided by (2/9) equals 9, minus 2 equals 7. So yes, that uses three 2s.
But is this considered valid? The problem says "using only 3 2s". The decimal with a repeating bar is considered a single 2, right? Because you write it as .2 with a bar over the 2, which is just one 2. So in that case, this would be a valid solution.
Alternatively, if decimal repeating isn't allowed, maybe another approach. Let me think again. What if we use exponents and concatenation? For example, 2^2 + 2 = 4 +2 =6. No. If we do 2^(2) + 2 =6. Still no. How about 2 + 2^2 =6. Same thing.
Wait, maybe using square roots in a different way. For instance, sqrt(2 + 2) + 2. sqrt(4) +2 = 2 +2 =4. Not helpful.
Wait, maybe using cube roots? But cube root of 8 is 2. But how to get 8. 2 + 2 + 2 =6. Not 8.
Wait, another thought. If I take 2 and write it as 2 in base 3, which is 2 in decimal. Not helpful.
Wait, perhaps using 2 in a different form, like binary. But 2 in binary is 10. Not sure.
Alternatively, using 2 as a subscript or superscript. For example, in hyperoperations or something. But that's probably too obscure.
Wait, here's another idea. If we use the combination of factorial and square root. For example, sqrt(2!) is sqrt(2) ≈1.414. Then 2 + 2 + sqrt(2!) ≈ 4.414. Not 7.
Alternatively, 2! + 2! + 2! =6. Still 6.
Wait, maybe using percentage. 200% is 2. But 200% + 200% + 200% = 600% =6. Still 6.
Hmm. Let's see if there's a way to get 7 using three 2s with more complex operations. For example, 2 + 2 + 2 =6. If we can do 6 +1 =7, but how to get 1 with a 2. Wait, 2 - 2/2 =1. But that uses three 2s. So 2 - 2/2 =1, but that's already three 2s. Then we can't add that to anything else.
Alternatively, maybe (2 + 2) - (2/2) =4 -1=3. Not helpful.
Wait, here's another approach. Using the reciprocal. 2 + 2 + 2 =6. 2 + 2 + 1/2 =4.5. Not helpful. 2 / (2/2) =2 /1=2. Not helpful.
Wait, what about using exponents with subtraction. For example, 2^(3) -1=8-1=7. But how to get 3 and 1 from 2s. 2 + 2/2 =3. So 2^(2 + 2/2) - (2/2) =8 -1=7. But that uses five 2s. Too many.
Wait, but if we can write 3 as 2 + 2/2, which uses three 2s, then 2^3=8, then subtract 1=2/2. So total that would be 2^(2 + 2/2) - 2/2 =8 -1=7. But how many 2s is that? Let's count: inside the exponent, 2 + (2/2) uses three 2s. Then the base is another 2, and the subtraction part is 2/2, which is two more 2s. So total is 2 (base) + 2 (first in exponent) + 2 (second in exponent) + 2 (numerator in subtraction) + 2 (denominator in subtraction) = five 2s. So that's way over.
So that doesn't work.
Wait, but maybe the problem allows combining digits? Like 22 divided by something. For example, 22/2 - something. 22/2 is 11. 11 - 2 -2=7. But that uses four 2s. So 22/2 -2 -2=7. But that's four 2s. Not allowed.
Alternatively, 22 divided by 2 minus 2. That's 11 -2=9. No. Not helpful.
Wait, another angle: Using decimal points and concatenation. Like 2.2 + 2.2 + 2.2=6.6. Not 7. But if we use 2.2 + 2.2 + 2.6=7, but we can't make 2.6 with a 2. Alternatively, 2.2 + 2.8=5, but again, can't make 2.8.
Wait, unless we use 2.2 concatenated with another 2, like 2.22 + 2 + 2. But 2.22 +2 +2=6.22. Not 7.
Alternatively, if we can use exponents with decimals. For example, 2.2^2 =4.84. Then 4.84 +2=6.84. Still not 7.
Hmm. I'm stuck. Maybe the solution is using a different mathematical concept. For example, using the floor or ceiling function. But I don't know if that's allowed. For instance, ceiling(2.2 +2 +2)=ceiling(6.2)=7. But does that count? The problem didn't specify if functions like ceiling are allowed. If so, then ceiling(2.2 +2 +2)=7. But that uses three 2s in 2.2 and two more in the additions. Wait, no. The 2.2 is one 2, the other two 2s. So total three 2s. Then ceiling(2.2 +2 +2)=ceiling(6.2)=7. So that would use three 2s: 2.2, 2, and 2. But is the decimal point and the ceiling function allowed? The problem says "using only 3 2s". It might depend on the interpretation. If decimal points and standard mathematical functions are allowed, then maybe. But this feels a bit like stretching the rules.
Alternatively, using the square function: (2)² + 2 + 2 =4 +2 +2=8. Too much.
Wait, here's another idea. Using the reciprocal of 2. 1/2=0.5. Then 2/0.5=4. 4 +2 +2=8. Still no.
Wait, 2/(.2) =10. Then 10 - (2 +2/2)=10 -3=7. Wait, that uses four 2s: 2/(.2) is two 2s (the 2 and the .2), then subtracting (2 + 2/2) is three more 2s. Total five. Not allowed.
Alternatively, 2/(.2) - 2/2=10 -1=9. Still not 7.
Wait, if we do 2/(.2) - 2 -2=10 -2 -2=6. Not helpful.
Hmm. Maybe the answer is using decimal repeating with the overline, as I thought earlier. So 2 divided by 0.\overline{2} minus 2 equals 7. Let me verify:
0.\overline{2} = 2/9.
So 2 divided by (2/9) = 2 * (9/2) =9.
9 minus 2=7.
So the expression is 2 / 0.\overline{2} - 2 =7.
Now, count the number of 2s: the first 2, the 2 in the decimal 0.\overline{2}, and the last 2. Total three 2s. The overline is a notation for repeating decimals, which is a standard mathematical symbol. So this seems to work. Therefore, the solution is 2 divided by 0.222... minus 2, which equals 7.
Alternatively, written with LaTeX:
\frac{2}{0.\overline{2}} - 2 = 7
Let me check this calculation again:
0.\overline{2} is equal to 2/9. So 2 divided by (2/9) is 2 * (9/2) =9. Then 9 minus 2 is 7. Yep, that works. And it uses three 2s: the numerator 2, the 2 in the repeating decimal, and the subtracted 2. So three 2s total.
Therefore, the answer is 2 divided by 0. repeating 2 (which is 2/9) minus 2 equals 7.
So, the final answer is \boxed{7}, achieved by
2
0.
2
‾
−
2
0.
2
2
−2.
To make the number 7 using only three 2s, we can use the following approach:
Utilize repeating decimal notation: The repeating decimal
0.
2
‾
0.
2
is equivalent to
2
9
9
2
.
Divide 2 by the repeating decimal: This gives
2
0.
2
‾
=
2
2
9
=
9
0.
2
2
=
9
2
2
=9.
Subtract 2 from the result:
9
−
2
=
7
9−2=7.
This method uses three 2s: one in the numerator, one in the repeating decimal, and one in the subtraction.
7
7
The expression is
2
0.
2
‾
−
2
0.
2
2
−2, which simplifies to 7.
给你看看deepshit的表现
Okay, so I need to figure out how to make the number 7 using only three 2s. Hmm, let's see. The problem says "using only 3 2s," so I can use the digits 2, 2, and 2, and combine them with mathematical operations. Alright, let's start thinking about different operations I can use.
First, the basic ones: addition, subtraction, multiplication, division. Maybe exponents or factorials? The problem doesn't specify any restrictions, so I guess those are allowed. Let me try combining them step by step.
If I just add them all together: 2 + 2 + 2 = 6. That's too low. Not enough. What if I multiply some and add? Like 2 * 2 + 2 = 4 + 2 = 6. Still 6. Hmm. Maybe subtract instead? 2 * 2 - 2 = 4 - 2 = 2. Nope, that's worse. What if I use division? Let's see. 2 + 2 + (2/2) would use a fourth 2, which I don't have. Wait, no, I can only use three 2s. So division might not help here unless I structure it differently.
Wait, maybe exponents. Let's try that. 2^2 + 2 = 4 + 2 = 6. Still 6. How about 2^(2 + 2) = 2^4 = 16. That's way too high. Maybe 2^3, but I don't have a 3. Wait, can I use the number 3? No, only 2s. So exponents, but how? Let me think. If I use 2 squared plus 2, but that's the same as before.
Factorials? 2! is 2. So 2! + 2! + 2! = 6. Still 6. If I do (2 + 2)! + 2 = 24 + 2 = 26. That's way too big. Maybe 2 + 2 + 2! = 2 + 2 + 2 = 6. Still same result. Hmm.
What if I use decimal points? Like 2.2 or something? The problem didn't specify if decimal points are allowed. If they are, maybe 2.2 + 2.2 + 2.2 = 6.6. Not 7. Close, but not quite. Alternatively, combining numbers. For example, 22 divided by 2. Let's see: 22 / 2 = 11. That's too high. How about 2/2 + 2 = 1 + 2 = 3. Still low.
Wait, maybe concatenation is allowed. Like putting two 2s together to make 22. If so, then maybe 22 divided by 2 minus something. Wait, 22 divided by 2 is 11. If I subtract 2, that's 9. If I add 2 instead, that's 13. Not helpful. Alternatively, 2 + 2 + 2 = 6. Hmm. What if I use square roots? Sqrt(2) is approximately 1.414. So sqrt(2) + sqrt(2) + 2. But that would be roughly 1.414 + 1.414 + 2 = 4.828. Still not 7. And also, does the problem allow square roots? It might be stretching the rules.
Wait, maybe using exponents and factorials together. Let's think. For example, 2^(2) + 2! = 4 + 2 = 6. Still 6. How about (2 + 2)! / 2 = 24 / 2 = 12. Still not 7. Hmm.
What if I use decimal fractions with exponents? Like 2^(2) + 2.2? But that would be 4 + 2.2 = 6.2. Still not 7. Maybe 2.2 * 2 + 2? That would be 4.4 + 2 = 6.4. Closer, but not there yet.
Wait, maybe combining operations in a different order. For example, 2 + (2 * 2) = 2 + 4 = 6. Nope. What if I do 2 * 2 * 2 = 8. Oh, that's 8. Close to 7. How can I subtract 1 from 8? But how do I get 1 from a 2? Wait, 2/2 is 1. But then I would need a fourth 2. Let's see: 2 * 2 * 2 - (2/2). But that's four 2s. Not allowed. So that's out.
Alternatively, maybe 2^3 - something, but again, 3 isn't allowed. Unless I can make 3 from two 2s. 2 + 2/2 = 3. But that uses three 2s. So then 2^(2 + 2/2) = 2^3 = 8. Then subtract 1? But again, how to get 1. Wait, this is getting complicated.
Wait, maybe using a different approach. Let's see. If I can use decimal points, maybe 2.2 + 2.2 + 2.2 = 6.6. Not 7. If I can concatenate two 2s into 22, then 22 divided by something. 22 - 2 = 20. 22 / 2 = 11. 22 + 2 = 24. Not helpful.
Wait, what if I use exponents with decimals. Like 2^(3) - 1 = 8 -1 =7. But how to get 3 and 1 from 2s. Alternatively, 2 squared plus 2 squared minus 1. But again, getting 1 from a 2. Maybe 2/2. But again, that would require extra 2s.
Hold on, maybe using factorial and division. Let's think. For example, (2 + 2)! / 2 - 2. But that would be 24 / 2 - 2 = 12 - 2 = 10. Still not 7. Alternatively, (2! + 2! + 2!) = 6. No.
Wait, here's an idea. If I take 2 and do a factorial, that's 2. Then another factorial? 2!! which is 2. Doesn't help. Wait, maybe 2 + 2 = 4, and then 4! is 24. 24 divided by 2 is 12. Still not 7. Hmm.
Wait, let's think outside the box. Maybe using square roots and exponents. For example, sqrt(2) is about 1.414. So sqrt(2) * sqrt(2) = 2. But that's just back to 2. Hmm.
What if I do something like 2^2 + 2 + 2. But that's four 2s. Wait, no. If I can use three 2s, let's see. Wait, 2 squared is 4, plus 2 plus 2 is 8. But that's four 2s again.
Wait, maybe using decimal fractions in a different way. For example, .2 as 0.2. But the problem says "using only 3 2s", so can I use a decimal like .2? That might count as using a 2. So maybe 2 + 2 + 2. But that's 6. Wait, 2 / .2 = 10. If I do 2 / .2 + 2, that would be 10 + 2 = 12. But that uses two 2s for the 0.2 and one more 2. So total three 2s? Wait, .2 is just one 2. So 2 / 0.2 is 10, using one 2 for the numerator and one for the decimal. Then adding another 2. So total three 2s: 2 / .2 + 2. Let me check that. Yes: 2 divided by 0.2 is 10, plus 2 is 12. But we need 7. Hmm. Not helpful.
Wait, maybe 2 + 2 / .2. That's 2 + 10 = 12. Still not 7. Alternatively, 2 * 2 / .2. That's 4 / 0.2 = 20. No.
Alternatively, if I use a repeating decimal? Like .2 repeating? But that might be more complicated and not sure if allowed.
Wait, what if I use exponents with decimals? For example, (2 + 2)^2 = 16. But that's four 2s. Wait, 2 + 2 is two 2s, then squared is another operation. Hmm, not sure.
Wait, here's another idea. Using logarithms? But that seems complicated and probably not allowed. For example, log base 2 of something. But that might be stretching the rules.
Alternatively, using square roots in exponents. For example, 2^(sqrt(2)) is roughly 2.665. But adding those up? Not helpful.
Wait, perhaps using subtraction and division. Let's see. For example, (2 * 2) - (2 / 2) = 4 - 1 = 3. But again, that uses four 2s. No.
Wait, maybe 2^2 + 2 + 2, but that's four 2s. Not allowed.
Hold on, maybe using a combination of operations with different precedences. For example, 2 + 2 + 2 = 6. Not enough. 2 * 2 + 2 = 6. Still no. 2 + 2 * 2 = 6. Hmm.
Wait, what if I use fractions. Like 2 + 2 + 2/2. But that's four 2s. So no. Alternatively, 22/2 - something. 22/2 is 11. 11 - 2 = 9. 11 - (2+2) = 7. Wait, 11 - (2+2) is 7. But that would be 22/2 - (2+2) = 11 - 4 = 7. Let's count the 2s: 22 uses two 2s, divided by 2 is another 2, so that's three 2s. Then subtracting (2+2) would be two more 2s. So total five 2s. No, that's way over. So that's not allowed.
Wait, maybe there's a different way to arrange them. Let's see. How about 2 + 2 + 2 = 6. Then, is there a way to turn that 6 into 7 with the same three 2s? Maybe not.
Wait, another thought: Using decimal concatenation. For instance, 2.2 + 2.2 + 2.6, but we can't make 2.6. Alternatively, 2.2 + 2.8, but again, how to get 2.8 with a 2. Maybe 2.2 + 2.2 + 2.2 = 6.6. Still not 7.
Wait, maybe using percentages? 2% as 0.02. But that seems too small. 2 + 2 + 2% = 4.02. Not helpful.
Alternatively, using 2 in different number bases. For example, if we interpret the numbers in base 3 or something. But the problem doesn't specify. That might be cheating.
Wait, here's a different approach. What if we use the factorial of a decimal? For example, (2 + 2/2)! = (2 +1)! = 3! = 6. But again, 6. And that uses three 2s: 2, 2/2. Wait, 2 + (2/2) = 3. Then 3! =6. So total three 2s. But that gives us 6, not 7. Hmm.
Wait, what about using a repeating decimal? Like 2.\overline{2} which is 2.222... But that's approximately 2.222, and adding another 2 would be 2.222 + 2 + 2 = 6.222. Not 7.
Alternatively, combining 2s with other mathematical symbols. Maybe square root symbols without numbers. Wait, but square root of what? If I take the square root of 2, that's still a 2 inside. So sqrt(2) + sqrt(2) + 2 is approximately 1.414 +1.414 +2 = 4.828. Not enough.
Wait, perhaps using the gamma function, which extends factorials. Gamma(3) = 2! = 2. But not helpful. Gamma(4) = 6. Still 6.
Hmm, this is getting frustrating. Let me think again. The key is to use exactly three 2s with any operations. Maybe there's a trick here. Let's check if someone else has encountered this before. Wait, I recall that sometimes people use the notation where they put a bar over a number to indicate repeating decimals, but does that help here? For example, .2 with a bar over it is 0.222..., which is 2/9. Then 2 / (2/9) = 9. But that uses two 2s. Then 9 - 2 = 7. So total three 2s: 2 / (.\overline{2}) - 2. Let's check: .\overline{2} is 2/9, so 2 divided by (2/9) is 9, then subtract 2 gives 7. But does the notation .\overline{2} count as using a single 2? Because the bar is an operator, not a digit. So maybe that's acceptable. So 2 / 0.\overline{2} - 2 = 9 -2 =7. Let's count the 2s: the 2 in the numerator, the 2 in the repeating decimal, and the 2 being subtracted. So three 2s. That might work. But is this a standard notation? The problem didn't specify whether repeating decimals are allowed, but if they are, this could be a solution.
Alternatively, using the decimal point and a bar for repeating, which is a common mathematical notation. So 0.\overline{2} is 0.222..., which is 2/9. Therefore, the calculation would be 2 divided by (2/9) equals 9, minus 2 equals 7. So yes, that uses three 2s.
But is this considered valid? The problem says "using only 3 2s". The decimal with a repeating bar is considered a single 2, right? Because you write it as .2 with a bar over the 2, which is just one 2. So in that case, this would be a valid solution.
Alternatively, if decimal repeating isn't allowed, maybe another approach. Let me think again. What if we use exponents and concatenation? For example, 2^2 + 2 = 4 +2 =6. No. If we do 2^(2) + 2 =6. Still no. How about 2 + 2^2 =6. Same thing.
Wait, maybe using square roots in a different way. For instance, sqrt(2 + 2) + 2. sqrt(4) +2 = 2 +2 =4. Not helpful.
Wait, maybe using cube roots? But cube root of 8 is 2. But how to get 8. 2 + 2 + 2 =6. Not 8.
Wait, another thought. If I take 2 and write it as 2 in base 3, which is 2 in decimal. Not helpful.
Wait, perhaps using 2 in a different form, like binary. But 2 in binary is 10. Not sure.
Alternatively, using 2 as a subscript or superscript. For example, in hyperoperations or something. But that's probably too obscure.
Wait, here's another idea. If we use the combination of factorial and square root. For example, sqrt(2!) is sqrt(2) ≈1.414. Then 2 + 2 + sqrt(2!) ≈ 4.414. Not 7.
Alternatively, 2! + 2! + 2! =6. Still 6.
Wait, maybe using percentage. 200% is 2. But 200% + 200% + 200% = 600% =6. Still 6.
Hmm. Let's see if there's a way to get 7 using three 2s with more complex operations. For example, 2 + 2 + 2 =6. If we can do 6 +1 =7, but how to get 1 with a 2. Wait, 2 - 2/2 =1. But that uses three 2s. So 2 - 2/2 =1, but that's already three 2s. Then we can't add that to anything else.
Alternatively, maybe (2 + 2) - (2/2) =4 -1=3. Not helpful.
Wait, here's another approach. Using the reciprocal. 2 + 2 + 2 =6. 2 + 2 + 1/2 =4.5. Not helpful. 2 / (2/2) =2 /1=2. Not helpful.
Wait, what about using exponents with subtraction. For example, 2^(3) -1=8-1=7. But how to get 3 and 1 from 2s. 2 + 2/2 =3. So 2^(2 + 2/2) - (2/2) =8 -1=7. But that uses five 2s. Too many.
Wait, but if we can write 3 as 2 + 2/2, which uses three 2s, then 2^3=8, then subtract 1=2/2. So total that would be 2^(2 + 2/2) - 2/2 =8 -1=7. But how many 2s is that? Let's count: inside the exponent, 2 + (2/2) uses three 2s. Then the base is another 2, and the subtraction part is 2/2, which is two more 2s. So total is 2 (base) + 2 (first in exponent) + 2 (second in exponent) + 2 (numerator in subtraction) + 2 (denominator in subtraction) = five 2s. So that's way over.
So that doesn't work.
Wait, but maybe the problem allows combining digits? Like 22 divided by something. For example, 22/2 - something. 22/2 is 11. 11 - 2 -2=7. But that uses four 2s. So 22/2 -2 -2=7. But that's four 2s. Not allowed.
Alternatively, 22 divided by 2 minus 2. That's 11 -2=9. No. Not helpful.
Wait, another angle: Using decimal points and concatenation. Like 2.2 + 2.2 + 2.2=6.6. Not 7. But if we use 2.2 + 2.2 + 2.6=7, but we can't make 2.6 with a 2. Alternatively, 2.2 + 2.8=5, but again, can't make 2.8.
Wait, unless we use 2.2 concatenated with another 2, like 2.22 + 2 + 2. But 2.22 +2 +2=6.22. Not 7.
Alternatively, if we can use exponents with decimals. For example, 2.2^2 =4.84. Then 4.84 +2=6.84. Still not 7.
Hmm. I'm stuck. Maybe the solution is using a different mathematical concept. For example, using the floor or ceiling function. But I don't know if that's allowed. For instance, ceiling(2.2 +2 +2)=ceiling(6.2)=7. But does that count? The problem didn't specify if functions like ceiling are allowed. If so, then ceiling(2.2 +2 +2)=7. But that uses three 2s in 2.2 and two more in the additions. Wait, no. The 2.2 is one 2, the other two 2s. So total three 2s. Then ceiling(2.2 +2 +2)=ceiling(6.2)=7. So that would use three 2s: 2.2, 2, and 2. But is the decimal point and the ceiling function allowed? The problem says "using only 3 2s". It might depend on the interpretation. If decimal points and standard mathematical functions are allowed, then maybe. But this feels a bit like stretching the rules.
Alternatively, using the square function: (2)² + 2 + 2 =4 +2 +2=8. Too much.
Wait, here's another idea. Using the reciprocal of 2. 1/2=0.5. Then 2/0.5=4. 4 +2 +2=8. Still no.
Wait, 2/(.2) =10. Then 10 - (2 +2/2)=10 -3=7. Wait, that uses four 2s: 2/(.2) is two 2s (the 2 and the .2), then subtracting (2 + 2/2) is three more 2s. Total five. Not allowed.
Alternatively, 2/(.2) - 2/2=10 -1=9. Still not 7.
Wait, if we do 2/(.2) - 2 -2=10 -2 -2=6. Not helpful.
Hmm. Maybe the answer is using decimal repeating with the overline, as I thought earlier. So 2 divided by 0.\overline{2} minus 2 equals 7. Let me verify:
0.\overline{2} = 2/9.
So 2 divided by (2/9) = 2 * (9/2) =9.
9 minus 2=7.
So the expression is 2 / 0.\overline{2} - 2 =7.
Now, count the number of 2s: the first 2, the 2 in the decimal 0.\overline{2}, and the last 2. Total three 2s. The overline is a notation for repeating decimals, which is a standard mathematical symbol. So this seems to work. Therefore, the solution is 2 divided by 0.222... minus 2, which equals 7.
Alternatively, written with LaTeX:
\frac{2}{0.\overline{2}} - 2 = 7
Let me check this calculation again:
0.\overline{2} is equal to 2/9. So 2 divided by (2/9) is 2 * (9/2) =9. Then 9 minus 2 is 7. Yep, that works. And it uses three 2s: the numerator 2, the 2 in the repeating decimal, and the subtracted 2. So three 2s total.
Therefore, the answer is 2 divided by 0. repeating 2 (which is 2/9) minus 2 equals 7.
So, the final answer is \boxed{7}, achieved by
2
0.
2
‾
−
2
0.
2
2
−2.
To make the number 7 using only three 2s, we can use the following approach:
Utilize repeating decimal notation: The repeating decimal
0.
2
‾
0.
2
is equivalent to
2
9
9
2
.
Divide 2 by the repeating decimal: This gives
2
0.
2
‾
=
2
2
9
=
9
0.
2
2
=
9
2
2
=9.
Subtract 2 from the result:
9
−
2
=
7
9−2=7.
This method uses three 2s: one in the numerator, one in the repeating decimal, and one in the subtraction.
7
7
The expression is
2
0.
2
‾
−
2
0.
2
2
−2, which simplifies to 7.
If printing money would end poverty, printing diplomas would end stupidity.
#15 Re: 我给你看一下copilot屎一样的表现
If printing money would end poverty, printing diplomas would end stupidity.
#16 Re: 我给你看一下copilot屎一样的表现
上次由 biggestballs 在 2025年 2月 23日 10:23 修改。
Devil doesn't need an advocate
#17 Re: 我给你看一下copilot屎一样的表现
2 / 0.\overline{2} - 2 =7. 太牛逼了赖美豪中 写了: 2025年 2月 23日 10:11 看到你的表现,我觉得你软的确可以用ai把马工都取代了。都是不识数啊
给你看看deepshit的表现
Okay, so I need to figure out how to make the number 7 using only three 2s. Hmm, let's see. The problem says "using only 3 2s," so I can use the digits 2, 2, and 2, and combine them with mathematical operations. Alright, let's start thinking about different operations I can use.
First, the basic ones: addition, subtraction, multiplication, division. Maybe exponents or factorials? The problem doesn't specify any restrictions, so I guess those are allowed. Let me try combining them step by step.
If I just add them all together: 2 + 2 + 2 = 6. That's too low. Not enough. What if I multiply some and add? Like 2 * 2 + 2 = 4 + 2 = 6. Still 6. Hmm. Maybe subtract instead? 2 * 2 - 2 = 4 - 2 = 2. Nope, that's worse. What if I use division? Let's see. 2 + 2 + (2/2) would use a fourth 2, which I don't have. Wait, no, I can only use three 2s. So division might not help here unless I structure it differently.
Wait, maybe exponents. Let's try that. 2^2 + 2 = 4 + 2 = 6. Still 6. How about 2^(2 + 2) = 2^4 = 16. That's way too high. Maybe 2^3, but I don't have a 3. Wait, can I use the number 3? No, only 2s. So exponents, but how? Let me think. If I use 2 squared plus 2, but that's the same as before.
Factorials? 2! is 2. So 2! + 2! + 2! = 6. Still 6. If I do (2 + 2)! + 2 = 24 + 2 = 26. That's way too big. Maybe 2 + 2 + 2! = 2 + 2 + 2 = 6. Still same result. Hmm.
What if I use decimal points? Like 2.2 or something? The problem didn't specify if decimal points are allowed. If they are, maybe 2.2 + 2.2 + 2.2 = 6.6. Not 7. Close, but not quite. Alternatively, combining numbers. For example, 22 divided by 2. Let's see: 22 / 2 = 11. That's too high. How about 2/2 + 2 = 1 + 2 = 3. Still low.
Wait, maybe concatenation is allowed. Like putting two 2s together to make 22. If so, then maybe 22 divided by 2 minus something. Wait, 22 divided by 2 is 11. If I subtract 2, that's 9. If I add 2 instead, that's 13. Not helpful. Alternatively, 2 + 2 + 2 = 6. Hmm. What if I use square roots? Sqrt(2) is approximately 1.414. So sqrt(2) + sqrt(2) + 2. But that would be roughly 1.414 + 1.414 + 2 = 4.828. Still not 7. And also, does the problem allow square roots? It might be stretching the rules.
Wait, maybe using exponents and factorials together. Let's think. For example, 2^(2) + 2! = 4 + 2 = 6. Still 6. How about (2 + 2)! / 2 = 24 / 2 = 12. Still not 7. Hmm.
What if I use decimal fractions with exponents? Like 2^(2) + 2.2? But that would be 4 + 2.2 = 6.2. Still not 7. Maybe 2.2 * 2 + 2? That would be 4.4 + 2 = 6.4. Closer, but not there yet.
Wait, maybe combining operations in a different order. For example, 2 + (2 * 2) = 2 + 4 = 6. Nope. What if I do 2 * 2 * 2 = 8. Oh, that's 8. Close to 7. How can I subtract 1 from 8? But how do I get 1 from a 2? Wait, 2/2 is 1. But then I would need a fourth 2. Let's see: 2 * 2 * 2 - (2/2). But that's four 2s. Not allowed. So that's out.
Alternatively, maybe 2^3 - something, but again, 3 isn't allowed. Unless I can make 3 from two 2s. 2 + 2/2 = 3. But that uses three 2s. So then 2^(2 + 2/2) = 2^3 = 8. Then subtract 1? But again, how to get 1. Wait, this is getting complicated.
Wait, maybe using a different approach. Let's see. If I can use decimal points, maybe 2.2 + 2.2 + 2.2 = 6.6. Not 7. If I can concatenate two 2s into 22, then 22 divided by something. 22 - 2 = 20. 22 / 2 = 11. 22 + 2 = 24. Not helpful.
Wait, what if I use exponents with decimals. Like 2^(3) - 1 = 8 -1 =7. But how to get 3 and 1 from 2s. Alternatively, 2 squared plus 2 squared minus 1. But again, getting 1 from a 2. Maybe 2/2. But again, that would require extra 2s.
Hold on, maybe using factorial and division. Let's think. For example, (2 + 2)! / 2 - 2. But that would be 24 / 2 - 2 = 12 - 2 = 10. Still not 7. Alternatively, (2! + 2! + 2!) = 6. No.
Wait, here's an idea. If I take 2 and do a factorial, that's 2. Then another factorial? 2!! which is 2. Doesn't help. Wait, maybe 2 + 2 = 4, and then 4! is 24. 24 divided by 2 is 12. Still not 7. Hmm.
Wait, let's think outside the box. Maybe using square roots and exponents. For example, sqrt(2) is about 1.414. So sqrt(2) * sqrt(2) = 2. But that's just back to 2. Hmm.
What if I do something like 2^2 + 2 + 2. But that's four 2s. Wait, no. If I can use three 2s, let's see. Wait, 2 squared is 4, plus 2 plus 2 is 8. But that's four 2s again.
Wait, maybe using decimal fractions in a different way. For example, .2 as 0.2. But the problem says "using only 3 2s", so can I use a decimal like .2? That might count as using a 2. So maybe 2 + 2 + 2. But that's 6. Wait, 2 / .2 = 10. If I do 2 / .2 + 2, that would be 10 + 2 = 12. But that uses two 2s for the 0.2 and one more 2. So total three 2s? Wait, .2 is just one 2. So 2 / 0.2 is 10, using one 2 for the numerator and one for the decimal. Then adding another 2. So total three 2s: 2 / .2 + 2. Let me check that. Yes: 2 divided by 0.2 is 10, plus 2 is 12. But we need 7. Hmm. Not helpful.
Wait, maybe 2 + 2 / .2. That's 2 + 10 = 12. Still not 7. Alternatively, 2 * 2 / .2. That's 4 / 0.2 = 20. No.
Alternatively, if I use a repeating decimal? Like .2 repeating? But that might be more complicated and not sure if allowed.
Wait, what if I use exponents with decimals? For example, (2 + 2)^2 = 16. But that's four 2s. Wait, 2 + 2 is two 2s, then squared is another operation. Hmm, not sure.
Wait, here's another idea. Using logarithms? But that seems complicated and probably not allowed. For example, log base 2 of something. But that might be stretching the rules.
Alternatively, using square roots in exponents. For example, 2^(sqrt(2)) is roughly 2.665. But adding those up? Not helpful.
Wait, perhaps using subtraction and division. Let's see. For example, (2 * 2) - (2 / 2) = 4 - 1 = 3. But again, that uses four 2s. No.
Wait, maybe 2^2 + 2 + 2, but that's four 2s. Not allowed.
Hold on, maybe using a combination of operations with different precedences. For example, 2 + 2 + 2 = 6. Not enough. 2 * 2 + 2 = 6. Still no. 2 + 2 * 2 = 6. Hmm.
Wait, what if I use fractions. Like 2 + 2 + 2/2. But that's four 2s. So no. Alternatively, 22/2 - something. 22/2 is 11. 11 - 2 = 9. 11 - (2+2) = 7. Wait, 11 - (2+2) is 7. But that would be 22/2 - (2+2) = 11 - 4 = 7. Let's count the 2s: 22 uses two 2s, divided by 2 is another 2, so that's three 2s. Then subtracting (2+2) would be two more 2s. So total five 2s. No, that's way over. So that's not allowed.
Wait, maybe there's a different way to arrange them. Let's see. How about 2 + 2 + 2 = 6. Then, is there a way to turn that 6 into 7 with the same three 2s? Maybe not.
Wait, another thought: Using decimal concatenation. For instance, 2.2 + 2.2 + 2.6, but we can't make 2.6. Alternatively, 2.2 + 2.8, but again, how to get 2.8 with a 2. Maybe 2.2 + 2.2 + 2.2 = 6.6. Still not 7.
Wait, maybe using percentages? 2% as 0.02. But that seems too small. 2 + 2 + 2% = 4.02. Not helpful.
Alternatively, using 2 in different number bases. For example, if we interpret the numbers in base 3 or something. But the problem doesn't specify. That might be cheating.
Wait, here's a different approach. What if we use the factorial of a decimal? For example, (2 + 2/2)! = (2 +1)! = 3! = 6. But again, 6. And that uses three 2s: 2, 2/2. Wait, 2 + (2/2) = 3. Then 3! =6. So total three 2s. But that gives us 6, not 7. Hmm.
Wait, what about using a repeating decimal? Like 2.\overline{2} which is 2.222... But that's approximately 2.222, and adding another 2 would be 2.222 + 2 + 2 = 6.222. Not 7.
Alternatively, combining 2s with other mathematical symbols. Maybe square root symbols without numbers. Wait, but square root of what? If I take the square root of 2, that's still a 2 inside. So sqrt(2) + sqrt(2) + 2 is approximately 1.414 +1.414 +2 = 4.828. Not enough.
Wait, perhaps using the gamma function, which extends factorials. Gamma(3) = 2! = 2. But not helpful. Gamma(4) = 6. Still 6.
Hmm, this is getting frustrating. Let me think again. The key is to use exactly three 2s with any operations. Maybe there's a trick here. Let's check if someone else has encountered this before. Wait, I recall that sometimes people use the notation where they put a bar over a number to indicate repeating decimals, but does that help here? For example, .2 with a bar over it is 0.222..., which is 2/9. Then 2 / (2/9) = 9. But that uses two 2s. Then 9 - 2 = 7. So total three 2s: 2 / (.\overline{2}) - 2. Let's check: .\overline{2} is 2/9, so 2 divided by (2/9) is 9, then subtract 2 gives 7. But does the notation .\overline{2} count as using a single 2? Because the bar is an operator, not a digit. So maybe that's acceptable. So 2 / 0.\overline{2} - 2 = 9 -2 =7. Let's count the 2s: the 2 in the numerator, the 2 in the repeating decimal, and the 2 being subtracted. So three 2s. That might work. But is this a standard notation? The problem didn't specify whether repeating decimals are allowed, but if they are, this could be a solution.
Alternatively, using the decimal point and a bar for repeating, which is a common mathematical notation. So 0.\overline{2} is 0.222..., which is 2/9. Therefore, the calculation would be 2 divided by (2/9) equals 9, minus 2 equals 7. So yes, that uses three 2s.
But is this considered valid? The problem says "using only 3 2s". The decimal with a repeating bar is considered a single 2, right? Because you write it as .2 with a bar over the 2, which is just one 2. So in that case, this would be a valid solution.
Alternatively, if decimal repeating isn't allowed, maybe another approach. Let me think again. What if we use exponents and concatenation? For example, 2^2 + 2 = 4 +2 =6. No. If we do 2^(2) + 2 =6. Still no. How about 2 + 2^2 =6. Same thing.
Wait, maybe using square roots in a different way. For instance, sqrt(2 + 2) + 2. sqrt(4) +2 = 2 +2 =4. Not helpful.
Wait, maybe using cube roots? But cube root of 8 is 2. But how to get 8. 2 + 2 + 2 =6. Not 8.
Wait, another thought. If I take 2 and write it as 2 in base 3, which is 2 in decimal. Not helpful.
Wait, perhaps using 2 in a different form, like binary. But 2 in binary is 10. Not sure.
Alternatively, using 2 as a subscript or superscript. For example, in hyperoperations or something. But that's probably too obscure.
Wait, here's another idea. If we use the combination of factorial and square root. For example, sqrt(2!) is sqrt(2) ≈1.414. Then 2 + 2 + sqrt(2!) ≈ 4.414. Not 7.
Alternatively, 2! + 2! + 2! =6. Still 6.
Wait, maybe using percentage. 200% is 2. But 200% + 200% + 200% = 600% =6. Still 6.
Hmm. Let's see if there's a way to get 7 using three 2s with more complex operations. For example, 2 + 2 + 2 =6. If we can do 6 +1 =7, but how to get 1 with a 2. Wait, 2 - 2/2 =1. But that uses three 2s. So 2 - 2/2 =1, but that's already three 2s. Then we can't add that to anything else.
Alternatively, maybe (2 + 2) - (2/2) =4 -1=3. Not helpful.
Wait, here's another approach. Using the reciprocal. 2 + 2 + 2 =6. 2 + 2 + 1/2 =4.5. Not helpful. 2 / (2/2) =2 /1=2. Not helpful.
Wait, what about using exponents with subtraction. For example, 2^(3) -1=8-1=7. But how to get 3 and 1 from 2s. 2 + 2/2 =3. So 2^(2 + 2/2) - (2/2) =8 -1=7. But that uses five 2s. Too many.
Wait, but if we can write 3 as 2 + 2/2, which uses three 2s, then 2^3=8, then subtract 1=2/2. So total that would be 2^(2 + 2/2) - 2/2 =8 -1=7. But how many 2s is that? Let's count: inside the exponent, 2 + (2/2) uses three 2s. Then the base is another 2, and the subtraction part is 2/2, which is two more 2s. So total is 2 (base) + 2 (first in exponent) + 2 (second in exponent) + 2 (numerator in subtraction) + 2 (denominator in subtraction) = five 2s. So that's way over.
So that doesn't work.
Wait, but maybe the problem allows combining digits? Like 22 divided by something. For example, 22/2 - something. 22/2 is 11. 11 - 2 -2=7. But that uses four 2s. So 22/2 -2 -2=7. But that's four 2s. Not allowed.
Alternatively, 22 divided by 2 minus 2. That's 11 -2=9. No. Not helpful.
Wait, another angle: Using decimal points and concatenation. Like 2.2 + 2.2 + 2.2=6.6. Not 7. But if we use 2.2 + 2.2 + 2.6=7, but we can't make 2.6 with a 2. Alternatively, 2.2 + 2.8=5, but again, can't make 2.8.
Wait, unless we use 2.2 concatenated with another 2, like 2.22 + 2 + 2. But 2.22 +2 +2=6.22. Not 7.
Alternatively, if we can use exponents with decimals. For example, 2.2^2 =4.84. Then 4.84 +2=6.84. Still not 7.
Hmm. I'm stuck. Maybe the solution is using a different mathematical concept. For example, using the floor or ceiling function. But I don't know if that's allowed. For instance, ceiling(2.2 +2 +2)=ceiling(6.2)=7. But does that count? The problem didn't specify if functions like ceiling are allowed. If so, then ceiling(2.2 +2 +2)=7. But that uses three 2s in 2.2 and two more in the additions. Wait, no. The 2.2 is one 2, the other two 2s. So total three 2s. Then ceiling(2.2 +2 +2)=ceiling(6.2)=7. So that would use three 2s: 2.2, 2, and 2. But is the decimal point and the ceiling function allowed? The problem says "using only 3 2s". It might depend on the interpretation. If decimal points and standard mathematical functions are allowed, then maybe. But this feels a bit like stretching the rules.
Alternatively, using the square function: (2)² + 2 + 2 =4 +2 +2=8. Too much.
Wait, here's another idea. Using the reciprocal of 2. 1/2=0.5. Then 2/0.5=4. 4 +2 +2=8. Still no.
Wait, 2/(.2) =10. Then 10 - (2 +2/2)=10 -3=7. Wait, that uses four 2s: 2/(.2) is two 2s (the 2 and the .2), then subtracting (2 + 2/2) is three more 2s. Total five. Not allowed.
Alternatively, 2/(.2) - 2/2=10 -1=9. Still not 7.
Wait, if we do 2/(.2) - 2 -2=10 -2 -2=6. Not helpful.
Hmm. Maybe the answer is using decimal repeating with the overline, as I thought earlier. So 2 divided by 0.\overline{2} minus 2 equals 7. Let me verify:
0.\overline{2} = 2/9.
So 2 divided by (2/9) = 2 * (9/2) =9.
9 minus 2=7.
So the expression is 2 / 0.\overline{2} - 2 =7.
Now, count the number of 2s: the first 2, the 2 in the decimal 0.\overline{2}, and the last 2. Total three 2s. The overline is a notation for repeating decimals, which is a standard mathematical symbol. So this seems to work. Therefore, the solution is 2 divided by 0.222... minus 2, which equals 7.
Alternatively, written with LaTeX:
\frac{2}{0.\overline{2}} - 2 = 7
Let me check this calculation again:
0.\overline{2} is equal to 2/9. So 2 divided by (2/9) is 2 * (9/2) =9. Then 9 minus 2 is 7. Yep, that works. And it uses three 2s: the numerator 2, the 2 in the repeating decimal, and the subtracted 2. So three 2s total.
Therefore, the answer is 2 divided by 0. repeating 2 (which is 2/9) minus 2 equals 7.
So, the final answer is \boxed{7}, achieved by
2
0.
2
‾
−
2
0.
2
2
−2.
To make the number 7 using only three 2s, we can use the following approach:
Utilize repeating decimal notation: The repeating decimal
0.
2
‾
0.
2
is equivalent to
2
9
9
2
.
Divide 2 by the repeating decimal: This gives
2
0.
2
‾
=
2
2
9
=
9
0.
2
2
=
9
2
2
=9.
Subtract 2 from the result:
9
−
2
=
7
9−2=7.
This method uses three 2s: one in the numerator, one in the repeating decimal, and one in the subtraction.
7
7
The expression is
2
0.
2
‾
−
2
0.
2
2
−2, which simplifies to 7.
提交的表单无效,请再提交一次。sever error
#18 Re: 我给你看一下copilot屎一样的表现
o-3 high有个超级牛b的,你可以是馊一下
If printing money would end poverty, printing diplomas would end stupidity.
#19 Re: 我给你看一下copilot屎一样的表现
There are two ways to conquer and enslave a country. One is by the sword. The other is by debt. - John Adams
#20 Re: 我给你看一下copilot屎一样的表现
你软的牛b在于我指出他不对以后,它可以把错误重复一次,表示这次肯定对了,这样的自信有着浓浓的班加罗尔咖喱味
x1
 x2
x2

 x2
x2

If printing money would end poverty, printing diplomas would end stupidity.