Galois group representation

[FoxMe]

我努力一下，看看能不能搞懂。

我也想知道。

[FoxMe]

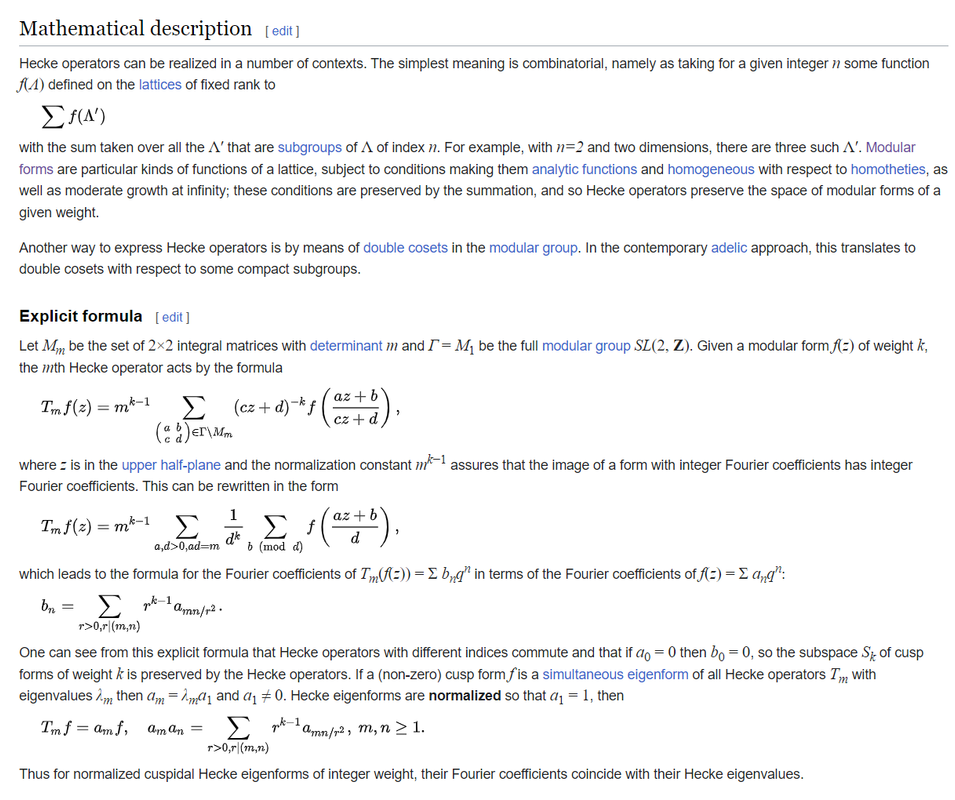
看了一下，这两种表述是等效的。对一种是在index=m的子格上的求和（或平均），第二种是行列式为m的矩阵上的求和，其实是一回事。

问题是在index=m的子格上的求和（或平均）是什么意义呢？想干啥？

Hecke operator 来了：

[FoxMe]

类似的求和在群表示论中也有，以前讨论过。是什么原因，忘了：

[TheMatrix]

看了一下，这两种表述是等效的。对一种是在index=m的子格上的求和（或平均），第二种是行列式为m的矩阵上的求和，其实是一回事。

问题是在index=m的子格上的求和（或平均）是什么意义呢？想干啥？

为的是使得到的算符可以作用在函数的傅里叶系数上。

比如函数f，它的傅里叶变换是f^{^}。现在定义一个算符H，那么Hf的傅里叶变换(Hf)^{^}，一般情况下，和f^{^}之间没有简单的关系。但是Hecke operator通过格上求平均的定义，(Hf)^{^}就可以和f^{^}之间有简单的关系。

[FoxMe]

哦，我还需要继续琢磨

为的是使得到的算符可以作用在函数的傅里叶系数上。

比如函数f，它的傅里叶变换是f^{^}。现在定义一个算符H，那么Hf的傅里叶变换(Hf)^{^}，一般情况下，和f^{^}之间没有简单的关系。但是Hecke operator通过格上求平均的定义，(Hf)^{^}就可以和f^{^}之间有简单的关系。

[FoxMe]

Galois group representation --> Artin L function --> Automorphic form (modular form的推广)

https://en.wikipedia.org/wiki/Artin_L-function

这就联系起来了: Langlands program

[FoxMe]

Galois group representation其实就是研究Galois群作用在（module等）线性结构上，说白了就是线性代数。以前有种说法是代数就是研究线性代数，看来是有一定道理的。

[TheMatrix]

Galois group representation其实就是研究Galois群作用在（module等）线性结构上，说白了就是线性代数。以前有种说法是代数就是研究线性代数，看来是有一定道理的。

我看到一个说法，说计算的第一步是线性代数，而所有的数学概念都要想办法开始计算，不能计算的相当于还没有办法去研究，所以线性代数是所有可研究的概念的第一步。也有道理。