模拟是线性减少的,而不是对数减少
版主: verdelite, TheMatrix
这些门牌号是1,2,3,……,一直到capacity?如果这样的话,首位数是9的概率自然比首位数是1的概率低。(ヅ) 写了: 2023年 1月 18日 19:32 假设100k个门牌号样本,对于每一条街,按照均匀分布随机有一个capacity\in [1, 1000],在这条街上有从1到capacity这么多个门牌号
模拟是线性减少的,而不是对数减少

维基上举例说电费、门牌号、股票价、房价等都遵循本福德定律(而且是对数下降),是不是因为(在这些实际情形中)小的capacity出现的概率更高些?模拟时可不可以在选capacity那一步微调一下,让小capacity出现的机率高些。我瞎猜的。(ヅ) 写了: 2023年 1月 18日 19:59 是的
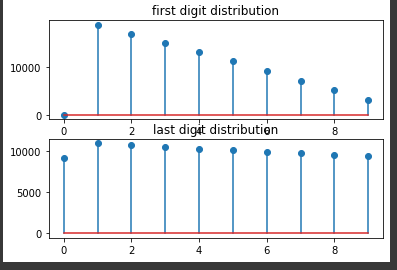
wiki上说是对数下降,我模拟是线性下降的(按照现有假设确实应该是线性)
https://en.wikipedia.org/wiki/Benford%27s_law
肯定哪儿有问题
我觉得他的意思是每个block从1开始增加,增加到某个capacity就完了,然后统计下一个blockYWY 写了: 2023年 1月 18日 20:21 维基上举例说电费、门牌号、股票价、房价等都遵循本福德定律(而且是对数下降),是不是因为(在这些实际情形中)小的capacity出现的概率更高些?模拟时可不可以在选capacity那一步微调一下,让小capacity出现的机率高些。我瞎猜的。
代码: 全选
import math
import random
import numpy as np
import matplotlib.pyplot as plt
# utility functions
def first_digit(n):
assert isinstance(n, int)
assert n >= 0
digit = n
while n > 0:
digit = n
n = int(n / 10)
return digit
def last_digit(n):
assert isinstance(n, int)
assert n >= 0
return n % 10
# CONSTANTS
N = 100000 # total number of samples
CAPACITY_UPPER_BOUND = 1000 # max number of street numbers at each block
n = 0
arr_first_digit = np.zeros(10)
arr_last_digit = np.zeros(10)
while n < N:
number_of_street_numbers = random.randint(1, CAPACITY_UPPER_BOUND)
for street_number in range(1, number_of_street_numbers + 1):
if n >= N:
break
f_d = first_digit(street_number)
arr_first_digit[f_d] = arr_first_digit[f_d] + 1
l_d = last_digit(street_number)
arr_last_digit[l_d] = arr_last_digit[l_d] + 1
n = n + 1
fig, (ax1, ax2) = plt.subplots(2)
ax1.stem(range(0, 10), arr_first_digit)
ax1.set_title("first digit distribution")
ax2.stem(range(0, 10), arr_last_digit)
ax2.set_title("last digit distribution")
plt.show()
我说的意思就是说在实际生活中,可能capacity不是均匀分布。比如门牌号受限于所在街道的建房的总数,但各个街道里建房的总数(可能)不是均匀分布。(ヅ) 写了: 2023年 1月 18日 20:25 我觉得他的意思是每个block从1开始增加,增加到某个capacity就完了,然后统计下一个block
这样如果capacity是均匀分布的,直观看首位数字应该是线性分布
要得到对数分布必定是我哪个假设有问题
贴下模拟代码,很简单,随便找个jupyter就能跑
代码: 全选
import math import random import numpy as np import matplotlib.pyplot as plt # utility functions def first_digit(n): assert isinstance(n, int) assert n >= 0 digit = n while n > 0: digit = n n = int(n / 10) return digit def last_digit(n): assert isinstance(n, int) assert n >= 0 return n % 10 # CONSTANTS N = 100000 # total number of samples CAPACITY_UPPER_BOUND = 1000 # max number of street numbers at each block n = 0 arr_first_digit = np.zeros(10) arr_last_digit = np.zeros(10) while n < N: number_of_street_numbers = random.randint(1, CAPACITY_UPPER_BOUND) for street_number in range(1, number_of_street_numbers + 1): if n >= N: break f_d = first_digit(street_number) arr_first_digit[f_d] = arr_first_digit[f_d] + 1 l_d = last_digit(street_number) arr_last_digit[l_d] = arr_last_digit[l_d] + 1 n = n + 1 fig, (ax1, ax2) = plt.subplots(2) ax1.stem(range(0, 10), arr_first_digit) ax1.set_title("first digit distribution") ax2.stem(range(0, 10), arr_last_digit) ax2.set_title("last digit distribution") plt.show()
你说的有道理YWY 写了: 2023年 1月 18日 20:34 我说的意思就是说在实际生活中,可能capacity不是均匀分布。比如门牌号受限于所在街道的建房的总数,但各个街道里建房的总数(可能)不是均匀分布。
不知用geometric distribution会怎么样。。。(ヅ) 写了: 2023年 1月 18日 20:37 你说的有道理
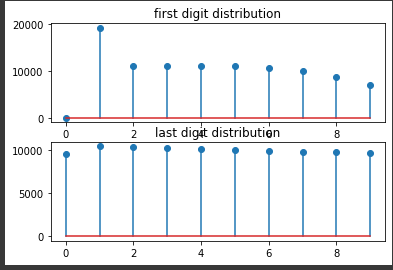
也许是以某个数为中心的正态分布更符合实际情况
试了一组参数,把
number_of_street_numbers = random.randint(1, CAPACITY_UPPER_BOUND)
替换成
number_of_street_numbers = int(np.random.normal(100, 20))
结果更离谱了
