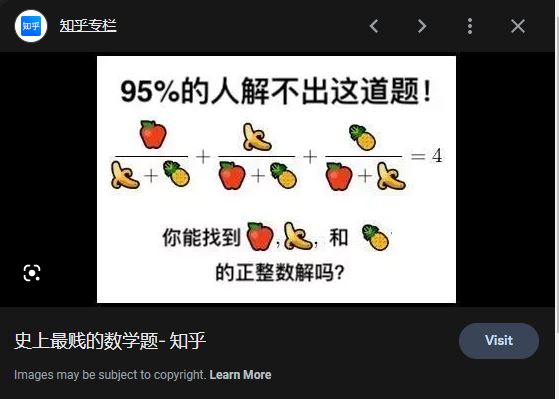
问,这个方程的整数解

[（ヅ）]

x / (y + z) + y / (z + x) + z / (x + y）= 4

齐次方程所以可以先锁定一个变量z = 1

相当有挑战的一个问题

[TheMatrix]

x / (y + z) + y / (z + x) + z / (x + y）= 4

这个剧大。

[Caravel]

x / (y + z) + y / (z + x) + z / (x + y）= 4

这个具有对称性

[rgg]

WolframAlpha 给我一组有负整数的解，不大也没对称性.

[Caravel]

WolframAlpha 给我一组有负整数的解，不大也没对称性.

解是多少？
对称性是说，x,y可以交换。

用群论的思路，应该吧这个方程改写成对称多项式，

ｘ＋ｙ+ z
xy, yz, xz
xyz

的方程

[verdelite]

这题可以用Python解。解出了一大堆答案，几百个都有了。先问问负数可以吗，例如4,11,-1。验算是对的。

Update: 搜索了x,y,z各300以内，结果没有找到正整数解。所以必须有负数吧。

[verdelite]

>>> for x in range(-100,100):
...    for y in range(-100,100):
...        for z in range(-100,100):
...            if x*(z+x)*(x+y) + y*(y+z)*(x+y)+z*(y+z)*(z+x)==4*(y+z)*(z+x)*(x+y) and z+x != 0 and x+y != 0 and y+z != 0:
...                 print(x,y,z)
...

-99 -81 45
-99 -36 9
-99 9 -36
-99 45 -81
-88 -72 40
-88 -32 8
-88 8 -32
-88 40 -72
-81 -99 45
-81 45 -99
-77 -63 35
-77 -28 7
-77 7 -28
-77 35 -63
-72 -88 40
-72 40 -88
-66 -54 30
-66 -24 6
-66 6 -24
-66 30 -54
-63 -77 35
-63 35 -77
-55 -45 25
-55 -20 5
-55 5 -20
-55 25 -45
-54 -66 30
-54 30 -66
-45 -55 25
-45 25 -55
-45 81 99
-45 99 81
-44 -36 20
-44 -16 4
-44 4 -16
-44 20 -36
-40 72 88
-40 88 72
-36 -99 9
-36 -44 20
-36 9 -99
-36 20 -44
-35 63 77
-35 77 63
-33 -27 15
-33 -12 3
-33 3 -12
-33 15 -27
-32 -88 8
-32 8 -88
-30 54 66
-30 66 54
-28 -77 7
-28 7 -77
-27 -33 15
-27 15 -33
-25 45 55
-25 55 45
-24 -66 6
-24 6 -66
-22 -18 10
-22 -8 2
-22 2 -8
-22 10 -18
-20 -55 5
-20 5 -55
-20 36 44
-20 44 36
-18 -22 10
-18 10 -22
-16 -44 4
-16 4 -44
-15 27 33
-15 33 27
-12 -33 3
-12 3 -33
-11 -9 5
-11 -4 1
-11 1 -4
-11 5 -9
-10 18 22
-10 22 18
-9 -11 5
-9 5 -11
-9 36 99
-9 99 36
-8 -22 2
-8 2 -22
-8 32 88
-8 88 32
-7 28 77
-7 77 28
-6 24 66
-6 66 24
-5 9 11
-5 11 9
-5 20 55
-5 55 20
-4 -11 1
-4 1 -11
-4 16 44
-4 44 16
-3 12 33
-3 33 12
-2 8 22
-2 22 8
-1 4 11
-1 11 4
1 -11 -4
1 -4 -11
2 -22 -8
2 -8 -22
3 -33 -12
3 -12 -33
4 -44 -16
4 -16 -44
4 -1 11
4 11 -1
5 -55 -20
5 -20 -55
5 -11 -9
5 -9 -11
6 -66 -24
6 -24 -66
7 -77 -28
7 -28 -77
8 -88 -32
8 -32 -88
8 -2 22
8 22 -2
9 -99 -36
9 -36 -99
9 -5 11
9 11 -5
10 -22 -18
10 -18 -22
11 -5 9
11 -1 4
11 4 -1
11 9 -5
12 -3 33
12 33 -3
15 -33 -27
15 -27 -33
16 -4 44
16 44 -4
18 -10 22
18 22 -10
20 -44 -36
20 -36 -44
20 -5 55
20 55 -5
22 -10 18
22 -2 8
22 8 -2
22 18 -10
24 -6 66
24 66 -6
25 -55 -45
25 -45 -55
27 -15 33
27 33 -15
28 -7 77
28 77 -7
30 -66 -54
30 -54 -66
32 -8 88
32 88 -8
33 -15 27
33 -3 12
33 12 -3
33 27 -15
35 -77 -63
35 -63 -77
36 -20 44
36 -9 99
36 44 -20
36 99 -9
40 -88 -72
40 -72 -88
44 -20 36
44 -4 16
44 16 -4
44 36 -20
45 -99 -81
45 -81 -99
45 -25 55
45 55 -25
54 -30 66
54 66 -30
55 -25 45
55 -5 20
55 20 -5
55 45 -25
63 -35 77
63 77 -35
66 -30 54
66 -6 24
66 24 -6
66 54 -30
72 -40 88
72 88 -40
77 -35 63
77 -7 28
77 28 -7
77 63 -35
81 -45 99
81 99 -45
88 -40 72
88 -8 32
88 32 -8
88 72 -40
99 -45 81
99 -9 36
99 36 -9
99 81 -45

[TheMatrix]

x / (y + z) + y / (z + x) + z / (x + y）= 4

齐次方程所以可以先锁定一个变量z = 1

相当有挑战的一个问题

应该是正整数解，可以负的话看来不难。

[（ヅ）]

应该是正整数解，可以负的话看来不难。

是的，正整数解呢？

[rgg]

是的，正整数解呢？

听你们一说我去搜了搜，原来是个网红题，消遣普通群众的。

[Bayoak]

听你们一说我去搜了搜，原来是个网红题，消遣普通群众的。

给个链接

[TheMatrix]

给个链接

[Caravel]

尼玛，这题比我想象的还要难。不过也不是没有收获，通过这几个月的群论学习，产生了一些视角，可以观察到解的对称性，和射影几何学以及对称多项式。虽然还远远没有能解决这个问题的地步，但是至少看到代数曲线的发展也是有逻辑的，不像以前那样不明觉厉。

[verdelite]

尼玛，这题比我想象的还要难。不过也不是没有收获，通过这几个月的群论学习，产生了一些视角，可以观察到解的对称性，和射影几何学以及对称多项式。虽然还远远没有能解决这个问题的地步，但是至少看到代数曲线的发展也是有逻辑的，不像以前那样不明觉厉。

一个人的天才崇拜来源于：1，不懂世人皆傻；2，不了解他所崇拜的天才（搞出成就的科学史）。

[TheMatrix]

尼玛，这题比我想象的还要难。不过也不是没有收获，通过这几个月的群论学习，产生了一些视角，可以观察到解的对称性，和射影几何学以及对称多项式。虽然还远远没有能解决这个问题的地步，但是至少看到代数曲线的发展也是有逻辑的，不像以前那样不明觉厉。

有理点的问题我在二次曲线上遇到过。平面几何问题经常碰到直线与圆的交点问题。用computer algebra证明的关键是不能有根式，相当于找有理点。椭圆曲线是三次方程，需要两个有理点才能交于第三个有理点。不知道能以什么方式扩展到高次方程。

[gousheng]

方程是对称的，我先设定y=z，得出x=6y=6z；同样可以得出另外两组解y=6z=6x；z=6x=6y

x / (y + z) + y / (z + x) + z / (x + y）= 4

齐次方程所以可以先锁定一个变量z = 1

相当有挑战的一个问题

[Caravel]

主题帖子quota用完了，尼玛，这个站规很不好，为了防一两个垃圾id惩罚所有人

[TheMatrix]

主题帖子quota用完了，尼玛，这个站规很不好，为了防一两个垃圾id惩罚所有人

主题贴quota是多少？我觉得只限制军版就好了，其他版不需要。

[YWY]

主题贴quota是多少？我觉得只限制军版就好了，其他版不需要。

有版主反映有人刷屏骂人，因此对发贴进行了比原来更严厉的限制：

每个ID24小时发表主题数限制为 10个，每个ID每小时发表回帖数限制为30个。
连续两个主题之间时间间隔为1分钟，连续两个帖子之间时间间隔为30秒。

新增限制：注册满1天才能发帖子
不少人认为7天太长了，改为了1天。


版主不受此限制。

[Caravel]

主题贴quota是多少？我觉得只限制军版就好了，其他版不需要。

十条，这个指标应该因人而异，像大部分tracking record 优良的ID不应该有限制。只需要限制那种新ID，或者很少发帖的ID，或者曾经有前科的ID