
这是我自己算的
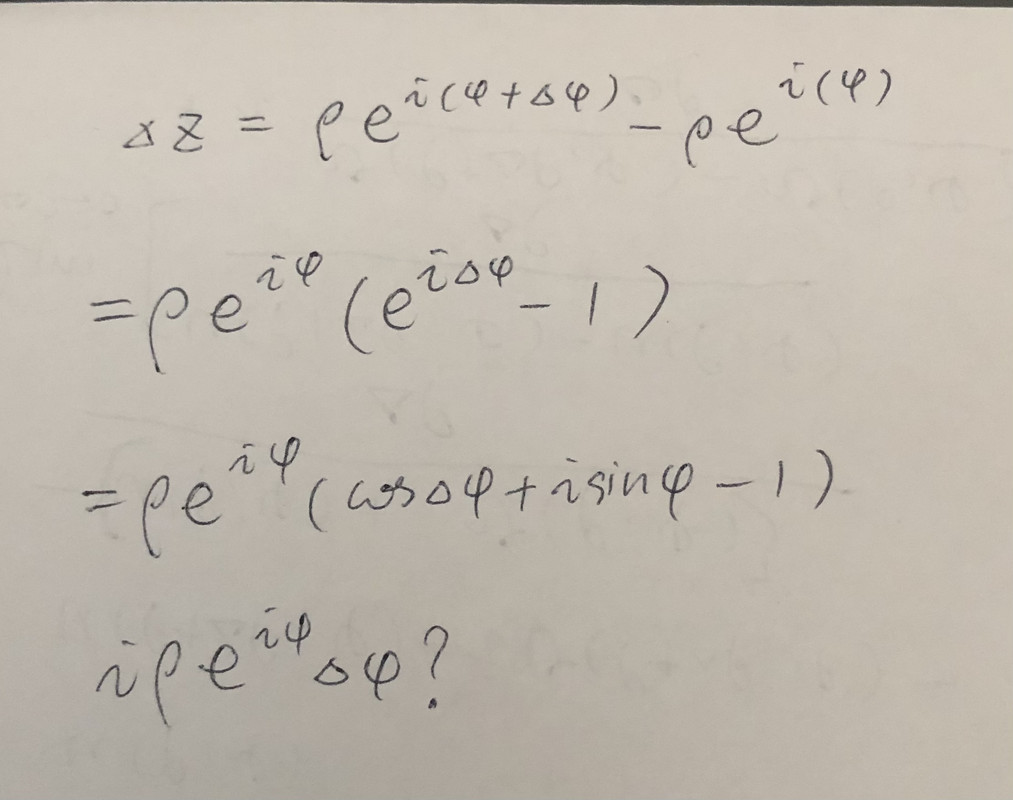
怎么对不上?!
版主: verdelite, TheMatrix
你忘了e^x的taylor series吧

cos x , sin x, 展开一下就知道了,一阶近似 cosx 等于1 , sinx 等于 x, 或者你对phi 求导也是一样的结果(ヅ) 写了: 2023年 1月 28日 18:24 你忘了e^x的taylor series吧
不过也没关系, i*sin(\delta \phi) (这里有个typo)
= i (x- 1/3!* (\delta \phi)^3 + 。。。)
cos(\delta\phi) - 1
= (1- 1/2 *(\delta\phi)^2+1/4! * x^4-\frac{1}{6!}(\delta\phi)^6 + ...) - 1
= - 1/2 *(\delta\phi)^2+1/4! * x^4-\frac{1}{6!}(\delta\phi)^6 + ...
那么cos(\delta \phi) + isin(\delta \phi) - 1
= i(\delta \phi) + O((\delta \phi)^2)
\approx i(\delta \phi)
你求导数偏导数的时候,只有(\delta \phi)的一次项留下来了,剩下的都是. 写完发现上面也有人说了
\lim_(\delta\phi \to 0) O((\delta \phi)^2) / (\delta \phi) = 0
