俺怎么觉得这是个很简单的问题。竟然被讨论个半天,还写code?
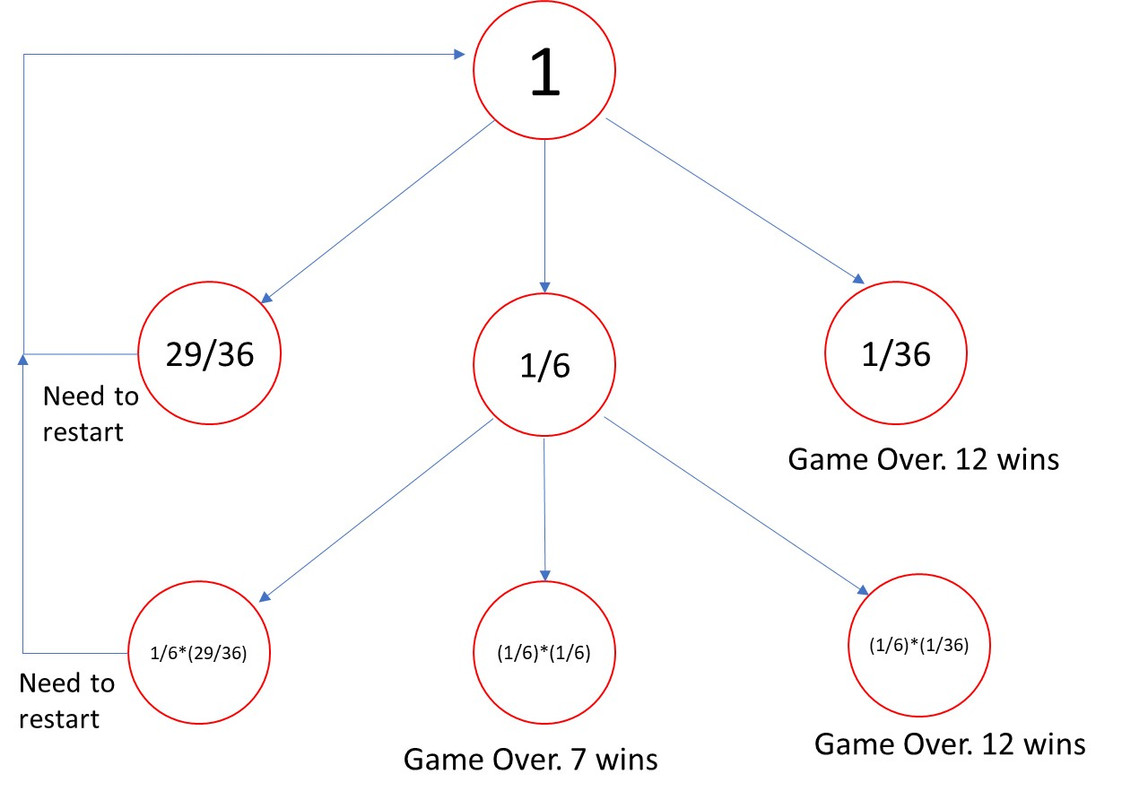
看下图,12 胜出的概率是1/36+1/216。7 胜出的概率是 1/36。
第一轮下来,如果是出现12,game over。出现7,需要继续第二轮。出现其他结果,等于game reset。
第二轮(如果第一轮出现的是7),出现7,7 胜出。出现12,还是12胜出。出现其他,等于game reset,重新开始。
俺的理解没问题吧?
版主: verdelite, TheMatrix

俺也没学过啥概率,不懂那些人讨论啥子了。
他们在算结束到7,7平均需要走几步。cheetah 写了: 2023年 2月 3日 10:49 俺也没学过啥概率,不懂那些人讨论啥子了。
图不是很容易理解吗?第一次走到最左边要清0重新开始的。或者第二次走到最左边也是要清0重新开始的(其实也就是第一次出了7,第二次出了非7、非12)等于头两次结果都不算数,大家重新开始了啊。
注意,几个leaf 节点概率相加是等于1的。说明最终停下来的状态的概率。
俺看那些讨论的热火朝天的,还要绕到第N次的,还要写code验证的,是不是读书读太多了,想得太复杂了?
楼主的这个循环图很漂亮,我很喜欢,但是,对于结果的解释还不够通俗。我看了大家的讨论,来做个自己的通俗解释。我们把这个循环图,看作是一个效率低下的二级榨油机,无限的运转,直到最终所有的油子变成最终油渣和麻油。cheetah 写了: 2023年 2月 3日 06:18 原题在:viewtopic.php?t=112971
俺怎么觉得这是个很简单的问题。竟然被讨论个半天,还写code?
看下图,12 胜出的概率是1/36+1/216。7 胜出的概率是 1/36。
第一轮下来,如果是出现12,game over。出现7,需要继续第二轮。出现其他结果,等于game reset。
第二轮(如果第一轮出现的是7),出现7,7 胜出。出现12,还是12胜出。出现其他,等于game reset,重新开始。
俺的理解没问题吧?

榨出的麻油分为两种:双7牌麻油、12号麻油。然后就可以讨论这两种麻油的比例。CalCat 写了: 2023年 2月 3日 14:09 楼主的这个循环图很漂亮,我很喜欢,但是,对于结果的解释还不够通俗。我看了大家的讨论,来做个自己的通俗解释。我们把这个循环图,看作是一个效率低下的二级榨油机,无限的运转,直到最终所有的油子变成最终油渣和麻油。
第一次榨油:通过第一级后,油子被分流成为3支:剩余油子(29/36), 初级油渣(1/6),麻油(1/36);通过第二级后,初级油渣被分流成为3支:剩余油子(1/6)(29/36), 最终油渣(1/6)(1/6),麻油(1/6)(1/36)。目前有麻油: (1/36)+ (1/6)(1/36)。
第二次榨油:前面两级过程中的剩余油子都反馈进入这个二级榨油机,总共的剩余油子(29/36)+(1/6)(29/36)。通过第二次榨油,得到的 麻油 [(29/36)+(1/6)(29/36)]*[(1/36)+ (1/6)(1/36))。
第三次次榨油:得到的 麻油 [(29/36)+(1/6)(29/36)]^2 *[(1/36)+ (1/6)(1/36))。
最终的麻油总量是把所有过程的相加:[(1/36)+ (1/6)(1/36))+ [(29/36)+(1/6)(29/36)]*[(1/36)+ (1/6)(1/36))]+ [(29/36)+(1/6)(29/36)]^2*[(1/36)+ (1/6)(1/36))]+ [(29/36)+(1/6)(29/36)]^3 *[(1/36)+ (1/6)(1/36))….
把这个无穷的麻油相加,得到最终结果。
当然一切取决于你自己的问题。但是,在你的另一个主贴里,你最开始问两种结果(双连7 vs. 12)的比例。想回答这个问题,就可以跟踪考虑双7牌麻油和12号麻油的产出比例。
叫油渣也好,叫双7牌麻油也罢,都无所谓。问题之一是这部分和12号麻油的产出比例,所以需要列在考虑范围内。当然了, 如果7/13的产出是12号麻油,但剩下的6/13自然就是双连7牌麻油(即你眼中的油渣)。
sorry 今天身体不适,没怎么上网。cheetah 写了: 2023年 2月 3日 06:18 原题在:viewtopic.php?t=112971
俺怎么觉得这是个很简单的问题。竟然被讨论个半天,还写code?
看下图,12 胜出的概率是1/36+1/216。7 胜出的概率是 1/36。
第一轮下来,如果是出现12,game over。出现7,需要继续第二轮。出现其他结果,等于game reset。
第二轮(如果第一轮出现的是7),出现7,7 胜出。出现12,还是12胜出。出现其他,等于game reset,重新开始。
俺的理解没问题吧?
