有趣的近似公式
发表于 : 2023年 7月 7日 22:27
sqrt(x^2 + y^2) ≈ 0.96x + 0.4y (原0.94 x + 0.4 y)
假设x >= y >= 0
精度(最大误差)在4%
还有哪些类似的近似公式?Doom的fast 1/sqrt(x)算最著名的吧
假设x >= y >= 0
精度(最大误差)在4%
还有哪些类似的近似公式?Doom的fast 1/sqrt(x)算最著名的吧
原文写错了,应该是0.96x + 0.4yYWY 写了: 2023年 7月 8日 02:33 When x = 1 and y = 0, then sqrt(x^2 + y^2) = 0 but 0.94 x + 0.4 y = 0.94, which is off by 6%.
When x = 1 and y = 1, then sqrt(x^2 + y^2) = sqrt(2) but 0.94 x + 0.4 y = 1.34, which is off by more than 5%.
I would rather use sqrt(x^2 + y^2) ≈ x + 0.4 y, where x >= y >= 0. Or maybe 1.1 x + 0.4 y is even better?
画一下图能看出,x + 0.4 y比0.96x + 0.4y更靠近sqrt(x^2 + y^2), where x >= y >= 0。
好奇Doom的fast 1/sqrt(x)是怎么表述的。。。
我用desmos画了,x + 0.4y当x = 1, y = 0.4的时候,sqrt(1+0.4^2) = 1.077, 1 + 0.4*0.4 = 1.16,相差7%YWY 写了: 2023年 7月 8日 11:47 画一下图能看出,x + 0.4 y比0.96x + 0.4y更靠近sqrt(x^2 + y^2), where x >= y >= 0。
因为考虑的是%误差,我们可以把近似式的两边同除以x,得到sqrt(1^2 + (y/x)^2) ≈ 1 + 0.4 y/x, where 1 >= y/x >=0。你给的近似式就是sqrt(1^2 + (y/x)^2) ≈ 0.96 + 0.4 y/x, where 1 >= y/x >=0。把y/x换成x,我们来对比下面两个近似表达
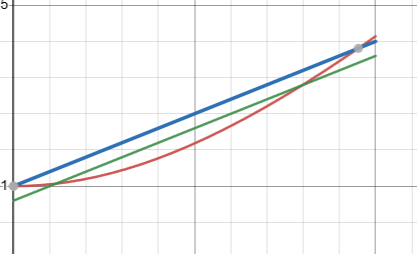
sqrt(1 + x^2) ≈ 1 + 0.4 x 和 sqrt(1 + x^2) ≈ 0.96 + 0.4 x, where 1 >= x >= 0.
通过在[0, 1]区间画sqrt(1 + x^2),1 + 0.4 x 和 0.96 + 0.4 x 这三个函数的图,能看出1 + 0.4 x更靠近sqrt(1 + x^2)。如果我们用稍大于1的数,误差%会更小,这也是sqrt(x^2 + y^2) ≈ 1.1 x + 0.4 y可能会更好的原因;当然1.1只是随手一写,可能1.06或1.12会更好一些。
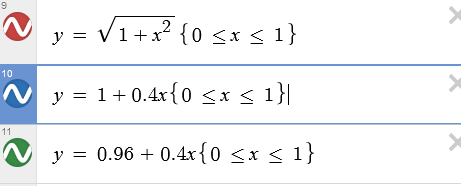
好的,我看看。
要算这个的原因是经常需要做归一化处理,(x, y, z) -> (x / sqrt(x^2 + y^2 + z^2), y / sqrt(x^2 + y^2 + z^2), z / sqrt(x^2 + y^2 + z^2))
谢画图解释!你是对的(ツ) 写了: 2023年 7月 8日 12:22 我用desmos画了,x + 0.4y当x = 1, y = 0.4的时候,sqrt(1+0.4^2) = 1.077, 1 + 0.4*0.4 = 1.16,相差7%
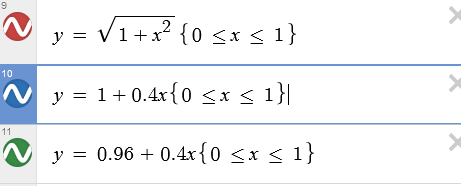
看了一下, 大知识用 x^{1/2} = 2^{log_2(x)/2}, 由于用的2,很多操作可以用 bit 的操作来实现。 当然为了避免数的溢出,需要做一些特殊处理。
(ツ) 写了: 2023年 7月 7日 22:27 sqrt(x^2 + y^2) ≈ 0.96x + 0.4y (原0.94 x + 0.4 y)
假设x >= y >= 0
精度(最大误差)在4%
还有哪些类似的近似公式?Doom的fast 1/sqrt(x)算最著名的吧
还以为Doom的fast 1/sqrt(x)是一个类似于sqrt(x^2 + y^2) ≈ 0.96x + 0.4y 的近似表达式,原来是个程序。看来人们为了避免根号和除法发明了很多手段,学习了。
好像你是需要速度,对精度要求不高(ツ) 写了: 2023年 7月 8日 12:32 要算这个的原因是经常需要做归一化处理,(x, y, z) -> (x / sqrt(x^2 + y^2 + z^2), y / sqrt(x^2 + y^2 + z^2), z / sqrt(x^2 + y^2 + z^2))
这个感觉不对劲,对 x y 不对称(ツ) 写了: 2023年 7月 7日 22:27 sqrt(x^2 + y^2) ≈ 0.96x + 0.4y (原0.94 x + 0.4 y)
假设x >= y >= 0
精度(最大误差)在4%
还有哪些类似的近似公式?Doom的fast 1/sqrt(x)算最著名的吧
是的,用分段一次函数会精度提高,失去了简洁
就是不失一般性假设。这样可以把整个\R^2平面上的定义域缩小到[0,1]\subset\R,方便讨论