分页: 1 / 2
#1 椭圆曲线的Conductor
发表于 : 2024年 3月 12日 17:45
由 TheMatrix
这个概念我一直没搞明白。有没有人能介绍一下?
#2 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 12日 18:29
由 FoxMe
同问。数域也有conductor。
#3 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 13日 07:39
由 forecasting
去搜搜吧,没想到简单例子。大约是椭圆曲线约化,如果是坏约化,则以约化曲线所在的素数p的奇点阶次幂(乘性奇点为1,即结点的次幂为1,而加性奇点次幂为2,即尖点的次幂为2)相乘得一值,此值为不变量,即所谓conductor
简单而抽象地说,就是把产生奇点的约化的素数模p依照奇点性质是结点(1)还是尖点(2)乘起来得到的值(也可以乘上好约化的p^0),如此就把所有约化奇点信息收集到一起了(编码到一个数值里面)
#4 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 13日 14:25
由 FoxMe
看了看,不好理解。
数域Q(zeta_n)的conductor=n.
#5 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 13日 16:34
由 TheMatrix
forecasting 写了: 2024年 3月 13日 07:39
去搜搜吧,没想到简单例子。大约是椭圆曲线约化,如果是坏约化,则以约化曲线所在的素数p的奇点阶次幂相乘得一值,此值为不变量,即所谓conductor
嗯。和reduction有关。
#6 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 13日 21:33
由 forecasting
FoxMe 写了: 2024年 3月 13日 14:25
看了看,不好理解。
数域Q(zeta_n)的conductor=n.
那是跟数域扩张有关的,不知道怎么跟椭圆曲线的约化和奇点联系起来
#7 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 15日 10:23
由 TheMatrix
#8 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 15日 15:52
由 TheMatrix
Discriminant Δ还是好理解的。
我是从分析的角度理解的:一个曲线和自己相交,或者在某一点其切线不唯一,这个条件是可以找出来的,是方程系数的一个关系。这就是Discriminant Δ。这是分析的角度。
代数的角度的话,我觉得就是把分析得来的关系直接用作定义。这就可以扩展到有理数系数上去了。
然后reduction at a prime。
比如Δ=875=5
3*7。那么,reduction at p=5的话,相当于Δ=0,因为modulo 5的时候,Δ就是等于0。这可以接受。
但是怎么就bad reduction了呢?
#9 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 15日 19:03
由 forecasting
TheMatrix 写了: 2024年 3月 15日 15:52
Discriminant Δ还是好理解的。
我是从分析的角度理解的:一个曲线和自己相交,或者在某一点其切线不唯一,这个条件是可以找出来的,是方程系数的一个关系。这就是Discriminant Δ。这是分析的角度。
代数的角度的话,我觉得就是把分析得来的关系直接用作定义。这就可以扩展到有理数系数上去了。
然后reduction at a prime。
比如Δ=875=5
3*7。那么,reduction at p=5的话,相当于Δ=0,因为modulo 5的时候,Δ就是等于0。这可以接受。
但是怎么就bad reduction了呢?
这是哪本书?
就是约化产生奇点的就是坏约化,或者wild reduction。顺便说一句,我要修改一下我第一个post了,含糊容易误解
#10 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 15日 19:09
由 TheMatrix
forecasting 写了: 2024年 3月 15日 19:03
这是哪本书?
就是约化产生奇点的就是坏约化,或者wild reduction。顺便说一句,我要修改一下我第一个post了,含糊容易误解
是Silverman的GTM那本书。
我主要是对singular point的代数定义没有理解。
#11 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 15日 19:55
由 forecasting
TheMatrix 写了: 2024年 3月 15日 19:09
是Silverman的GTM那本书。
我主要是对singular point的代数定义没有理解。
不知道奇点还有代数定义。
#12 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 15日 21:01
由 TheMatrix
#13 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 15日 21:36
由 TheMatrix
TheMatrix 写了: 2024年 3月 15日 21:01
E/Q的singular point怎么定义的?
来看看这个椭圆曲线:
y
2=x
3+x+2
x
3+ax+b with a=1,b=2
Δ=4a
3+27b
2=112=2
4*7
7是这个曲线的bad reduction。
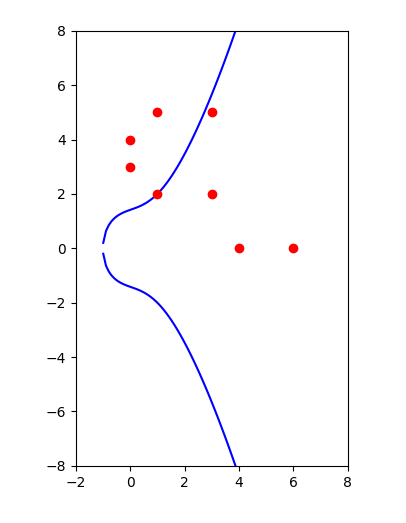
曲线mod 7有8个解,图上用红点表示:
(0, 3)
(0, 4)
(1, 2)
(1, 5)
(3, 2)
(3, 5)
(4, 0)
(6, 0)
其中哪个点是singular point?
#16 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 16日 05:47
由 forecasting
TheMatrix 写了: 2024年 3月 15日 21:01
E/Q的singular point怎么定义的?
素理想在扩张的域中的分歧指数?素理想对应到黎曼面的素点,进而对应到分歧点?由分歧点引出奇点?
我也是才想到应该是这样定义的。
#17 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 16日 07:26
由 forecasting
咋一看,都无比复杂困难,其实都是一些很直观的东西冠上了吓人的名字,主要是定义抽象,不说来龙去脉。
#18 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 16日 08:54
由 TheMatrix
TheMatrix 写了: 2024年 3月 15日 21:36
来看看这个椭圆曲线:
y
2=x
3+x+2
x
3+ax+b with a=1,b=2
Δ=4a
3+27b
2=112=2
4*7
7是这个曲线的bad reduction。
曲线mod 7有8个解,图上用红点表示:
(0, 3)
(0, 4)
(1, 2)
(1, 5)
(3, 2)
(3, 5)
(4, 0)
(6, 0)
其中哪个点是singular point?
从定义来看,椭圆曲线的singular point就是满足:
f(x,y)=y
2-(x
3+ax+b)=0
∂f/∂x=∂f/∂y=0
的点。
所以mod 7的8个解中,(4,0)点为singular point。
不过我看不到它的几何/分析意义。
#19 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 16日 08:55
由 TheMatrix
forecasting 写了: 2024年 3月 16日 05:47
素理想在扩张的域中的分歧指数?素理想对应到黎曼面的素点,进而对应到分歧点?由分歧点引出奇点?
我也是才想到应该是这样定义的。
哦。我说的E/Q就是指椭圆曲线,over Q的。
#20 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 17日 17:33
由 TheMatrix
TheMatrix 写了: 2024年 3月 16日 08:54
从定义来看,椭圆曲线的singular point就是满足:
f(x,y)=y
2-(x
3+ax+b)=0
∂f/∂x=∂f/∂y=0
的点。
所以mod 7的8个解中,(4,0)点为singular point。
不过我看不到它的几何/分析意义。
又理解了一点:
以 y
2=x
3+ax+b 的形式来看椭圆曲线的话,singular point如果存在,必然在x轴上,也就是y=0。而且是曲线两次通过x轴的点,也就是x
3+ax+b的double root。也就是方程能写成 y
2=(x-x
0)
2(x+x
1)的形式。那么(x
0,0)就是椭圆曲线的singular point。只能有一个singular point,而且x
0必然是实数。x
1也必然是实数,而且还要非负。
平移到使x
0=0的地方,方程变为y
2=x
2(x+x
1)。可以求出singular point处两条切线的斜率为 ±√x
1。如果x
1不等于0,那么两条切线不同,这样的singular point叫node。如果x
1等于0,那么两条切线重合,这样的singular point叫cusp。
这些条件从纯代数的角度看,也都是可以说得通的。这里只涉及到多项式因式分解,以及formal derivative。所以在有理数域,甚至有限数域的情况下,这些条件都可以说。这应该就成了good/bad reduction,以及bad reduction的node和cusp分类的定义。
#21 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 17日 22:46
由 TheMatrix
y
2=x
3-3x+2
变为
x
3-3x+2-y
2=0
看曲面 z=f(x,y)=x
3-3x+2-y
2 的形状:
z=0就是图中黄蓝交接的曲线。它有一个singular point,在红色圆圈的中心。这个奇点在曲面上是一个马鞍点。
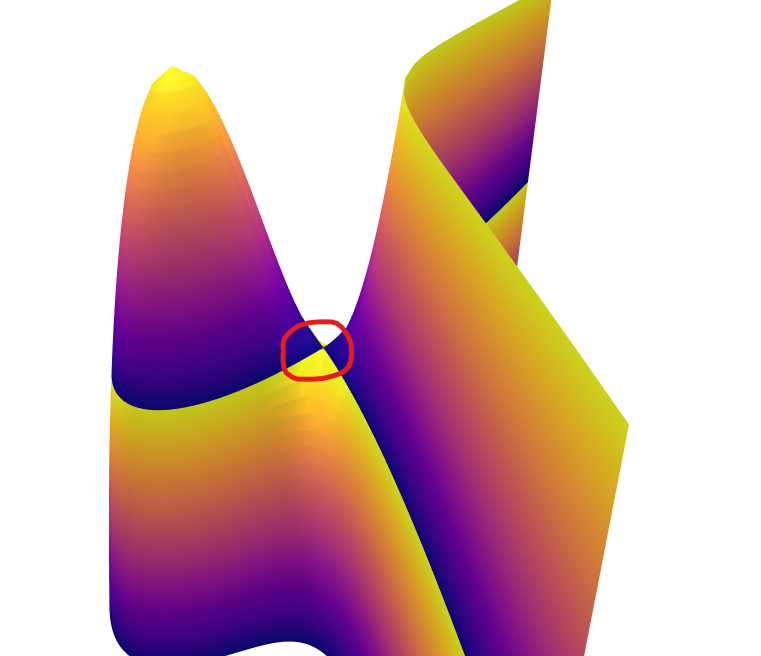
从斜上方看:
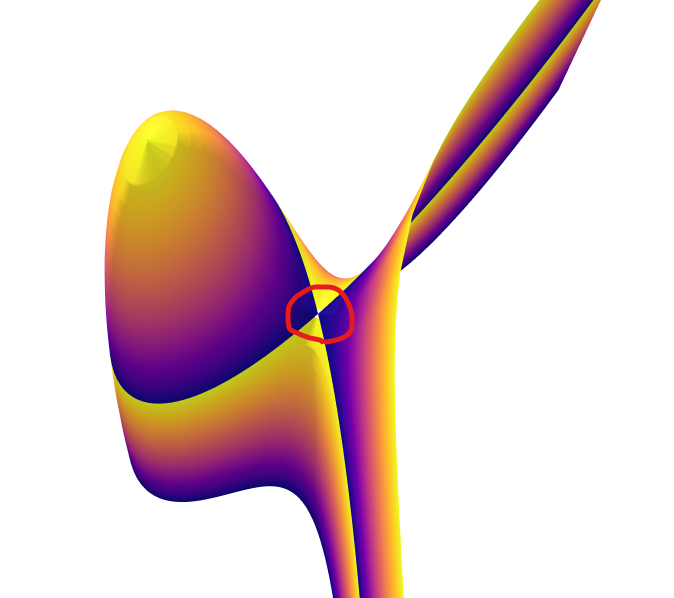
#22 Re: 椭圆曲线的Conductor
发表于 : 2024年 3月 17日 23:21
由 forecasting
TheMatrix 写了: 2024年 3月 17日 17:33
又理解了一点:
以 y
2=x
3+ax+b 的形式来看椭圆曲线的话,singular point如果存在,必然在x轴上,也就是y=0。而且是曲线两次通过x轴的点,也就是x
3+ax+b的double root。也就是方程能写成 y
2=(x-x
0)
2(x+x
1)的形式。那么(x
0,0)就是椭圆曲线的singular point。只能有一个singular point,而且x
0必然是实数。x
1也必然是实数,而且还要非负。
平移到使x
0=0的地方,方程变为y
2=x
2(x+x
1)。可以求出singular point处两条切线的斜率为 ±√x
1。如果x
1不等于0,那么两条切线不同,这样的singular point叫node。如果x
1等于0,那么两条切线重合,这样的singular point叫cusp。
这些条件从纯代数的角度看,也都是可以说得通的。这里只涉及到多项式因式分解,以及formal derivative。所以在有理数域,甚至有限数域的情况下,这些条件都可以说。这应该就成了good/bad reduction,以及bad reduction的node和cusp分类的定义。
椭圆曲线的奇点不依赖于坐标选择。引入特定坐标也只因为理解方便,还得小心带进去一些容易误解的东西。