Sheaf and Functor demystified

[TheMatrix]

Sheaf 就是 functor，一个特殊的 functor。

Functor就是function，可以按照function来理解，加一些限制或扩展。因为function比较容易理解。

Functor就是一个Category C的object的集合，到另一个Category D的object集合，的function。加一些限制和扩展。这不就容易理解了吗？

当然，据说一个Category的object collection可以比集合大，所以说要扩展一下。但是就这么理解就可以。

Functor还要加一些限制，比如它尊重各自Category中的箭头关系。但是function一般也要加限制，比如说连续函数，单增函数，这都不是裸函数，是在裸函数上加一些限制，使其尊重自变量集合和因变量集合中的某些关系。所以说把functor当作function来理解没什么问题。

Sheaf就是functor，也就是一个function。它有什么限制呢？首先，它的自变量是一个空间X的拓扑。什么叫一个空间的拓扑？就是一个空间的开集的集合。也就是Sheaf的自变量是X上的一个个开集。所以说它是一个特殊的functor，因为它的自变量集合定了。反过来，不是所有的functor都是Sheaf，因为只有自变量集合是一个空间的拓扑的functor才叫Sheaf。

[wildthing]

Sheaf 就是 functor，一个特殊的 functor。

Functor就是function，可以按照function来理解，加一些限制或扩展。因为function比较容易理解。

Functor就是一个Category C的object的集合，到另一个Category D的object集合，的function。加一些限制和扩展。这不就容易理解了吗？

当然，据说一个Category的object collection可以比集合大，所以说要扩展一下。但是就这么理解就可以。

Functor还要加一些限制，比如它尊重各自Category中的箭头关系。但是function一般也要加限制，比如说连续函数，单增函数，这都不是裸函数，是在裸函数上加一些限制，使其尊重自变量集合和因变量集合中的某些关系。所以说把functor当作function来理解没什么问题。

Sheaf就是functor，也就是一个function。它有什么限制呢？首先，它的自变量是一个空间X的拓扑。什么叫一个空间的拓扑？就是一个空间的开集的集合。也就是Sheaf的自变量是X上的一个个开集。所以说它是一个特殊的functor，因为它的自变量集合定了。反过来，不是所有的functor都是Sheaf，因为只有自变量集合是一个空间的拓扑的functor才叫Sheaf。

Functor is not function. It is a homomorphism of catergories.

But I have no good understand of functors in category theory.

All I know is that:

If f :: a -> b, then

fmap f :: F a -> F b, where F is a functor like Maybe or List or Tree.

[TheMatrix]

Functor is not function. It is a homomorphism of catergories.

But I have no good understand of functors in category theory.

All I know is that:

If f :: a -> b, then

fmap f :: F a -> F b, where F is a functor like Maybe or List or Tree.

哦，你这个是Haskell。我也玩过几天。

Functor 可以按照 function 来理解，加一些限制。Maybe可以理解成一个函数，Maybe(a)。I bet that’s how it’s implemented.

[forecasting]

Sheaf 就是 functor，一个特殊的 functor。

Functor就是function，可以按照function来理解，加一些限制或扩展。因为function比较容易理解。

Functor就是一个Category C的object的集合，到另一个Category D的object集合，的function。加一些限制和扩展。这不就容易理解了吗？

当然，据说一个Category的object collection可以比集合大，所以说要扩展一下。但是就这么理解就可以。

Functor还要加一些限制，比如它尊重各自Category中的箭头关系。但是function一般也要加限制，比如说连续函数，单增函数，这都不是裸函数，是在裸函数上加一些限制，使其尊重自变量集合和因变量集合中的某些关系。所以说把functor当作function来理解没什么问题。

Sheaf就是functor，也就是一个function。它有什么限制呢？首先，它的自变量是一个空间X的拓扑。什么叫一个空间的拓扑？就是一个空间的开集的集合。也就是Sheaf的自变量是X上的一个个开集。所以说它是一个特殊的functor，因为它的自变量集合定了。反过来，不是所有的functor都是Sheaf，因为只有自变量集合是一个空间的拓扑的functor才叫Sheaf。

你可以这样理解，的确有一些相似。但是collection不是集合，functor的确也不是function。集合，class，collection之间在做数学基础的人那里区别不小。混为一谈，会引起那些麻烦的悖论什么的。

[FoxMe]

我觉得可以这么理解。functor, morphism这些都是映射，可以说是广义的函数；函数也是映射。

Morphism是category之内的，functor是category之间的，它们都要遵循一定的规律，保持代数结构。

“Sheaf就是functor”，这个我还不知道。Sheaf也是一种映射。

Sheaf 就是 functor，一个特殊的 functor。

Functor就是function，可以按照function来理解，加一些限制或扩展。因为function比较容易理解。

Functor就是一个Category C的object的集合，到另一个Category D的object集合，的function。加一些限制和扩展。这不就容易理解了吗？

当然，据说一个Category的object collection可以比集合大，所以说要扩展一下。但是就这么理解就可以。

Functor还要加一些限制，比如它尊重各自Category中的箭头关系。但是function一般也要加限制，比如说连续函数，单增函数，这都不是裸函数，是在裸函数上加一些限制，使其尊重自变量集合和因变量集合中的某些关系。所以说把functor当作function来理解没什么问题。

Sheaf就是functor，也就是一个function。它有什么限制呢？首先，它的自变量是一个空间X的拓扑。什么叫一个空间的拓扑？就是一个空间的开集的集合。也就是Sheaf的自变量是X上的一个个开集。所以说它是一个特殊的functor，因为它的自变量集合定了。反过来，不是所有的functor都是Sheaf，因为只有自变量集合是一个空间的拓扑的functor才叫Sheaf。

[forecasting]

我记得collection汉语翻译作搜集。class翻译作类。当然两者都跟集合有区别。Sheaf翻译作层，层可以是但未必一定是函数。

[wildthing]

哦，你这个是Haskell。我也玩过几天。

Functor 可以按照 function 来理解，加一些限制。Maybe可以理解成一个函数，Maybe(a)。I bet that’s how it’s implemented.

Maybe is a functor, not a function.

Functor is a typeclass (or a class of types) in functional languages.

In terms of generality, we have

Functor :> Applicative :> Arrow :> Monad

[TheMatrix]

你可以这样理解，的确有一些相似。但是collection不是集合，functor的确也不是function。集合，class，collection之间在做数学基础的人那里区别不小。混为一谈，会引起那些麻烦的悖论什么的。

我这是非常简单粗暴的理解。主要是demystify for myself。但是也不能说是错，因为我说了“有一些扩展和限制”。我没说是什么扩展和限制，所有都在里面了。

[wildthing]

我这是非常简单粗暴的理解。主要是demystify for myself。但是也不能说是错，因为我说了“有一些扩展和限制”。我没说是什么扩展和限制，所有都在里面了。

Much smarter people find category theory hard to understand including people who can write compiler for quantum computers.

[forecasting]

Maybe is a functor, not a function.

Functor is a typeclass (or a class of types) in functional languages.

In terms of generality, we have

Functor :> Applicative :> Arrow :> Monad

你们说的是两个事情，相关而已。矩阵说的是数学里的funcor，范畴论里的。你说的是编程语言里的。在λ定义和演算里，两者有交集，但不同，数学的宽，编程语言里的窄多了，其实就是把λ定义和演算变成编程语言。

[TheMatrix]

Much smarter people find category theory hard to understand including people who can write compiler for quantum computers.

所以需要demistify。

Category theory的基本知识我觉得算是好的抽象。好的抽象都是有来源的，是为了解决痛点的。

[forecasting]

所以需要demistify。

Category theory的基本知识我觉得算是好的抽象。好的抽象都是有来源的，是为了解决痛点的。

啥好的抽象，就是类比，把集合变成了带着结构的object，把映射或者同构同态等变成了结构间的射等等，换个名词把已有的东西再玩一遍，全是一些大实话，老生常谈，因此没有新玩意。所以你 才觉得似曾相识。一向不严肃地看，有点蔑视这些花架子。

[TheMatrix]

我觉得可以这么理解。functor, morphism这些都是映射，可以说是广义的函数；函数也是映射。

Morphism是category之内的，functor是category之间的，它们都要遵循一定的规律，保持代数结构。

“Sheaf就是functor”，这个我还不知道。Sheaf也是一种映射。

Sheaf就是functor。Sheaf是 contravariant functor on a topological space。一个空间X的拓扑可以看作是一个category T：object是开集，morphism是开集之间的inclusion关系。

Sheaf是T上的functor。但是它没说这个functor的target是哪。Target可以是module of functions，这是一个category。也就是每一个开集上的全部function，这是一个module。这种情况可以说sheaf of module，或者sheaf of function。Target还可以是group。还可以是ring。可以说Sheaf of group, sheaf of ring。

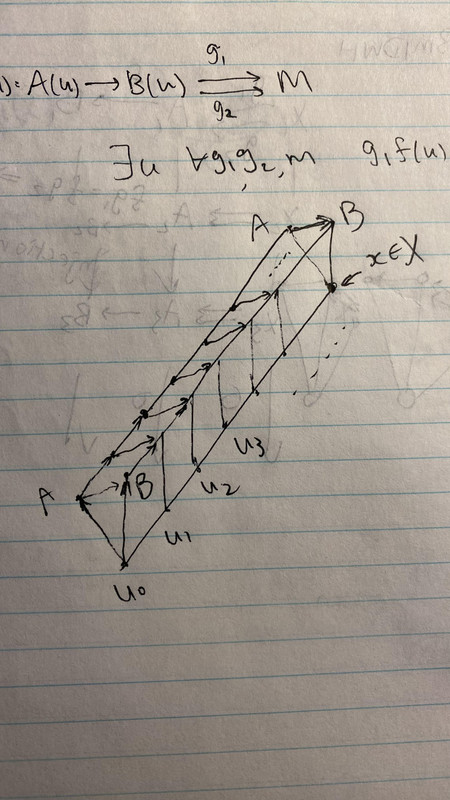
为什么要有sheaf这个概念呢？我觉得是为了研究每个点local的性质：一个点“附近”有多少种函数。所以就有了stalk的概念：一个点 x ∈ X，找到一个sequence of open sets：x ∈ ... U₃ ⊆ U₂ ⊆ U₁ ⊆ U₀=X。每一个开集都对应一个module of functions，然后求极限，这跟函数的极限也很像，就得到 sheaf stalk at x。

Sheaf就是为了研究stalk，意思是说sheaf之间的关系是从stalk来定义的。比如两个sheaf S₁ --> S₂，它的injection定义为在所有stalk上为injection。

[TheMatrix]

啥好的抽象，就是类比，把集合变成了带着结构的object，把映射或者同构同态等变成了结构间的射等等，换个名词把已有的东西再玩一遍，全是一些大实话，老生常谈，因此没有新玩意。所以你 才觉得似曾相识。一向不严肃地看，有点蔑视这些花架子。

能够把语言压缩，把很多种情况用一种方式统一地说出来，这就是意义。而且有足够多的用例，这就应该说是好的抽象。

[forecasting]

数学里就是运算和关系，运算或者函数（后来引进多值函数）是一对一的映射，关系就未必了。再加上元素，然后拿元素，运算/函数，关系这三个玩意玩就是，你觉得哪类/种元素，运算/函数，关系这三个玩意有意思，就单独列出来说一通。

[forecasting]

Sheaf就是functor。Sheaf是 contravariant functor on a topological space。一个空间X的拓扑可以看作是一个category T：object是开集，morphism是开集之间的inclusion关系。

Sheaf是T上的functor。但是它没说这个functor的target是哪。Target可以是module of functions，这是一个category。也就是每一个开集上的全部function，这是一个module。这种情况可以说sheaf of module，或者sheaf of function。Target还可以是group。还可以是ring。可以说Sheaf of group, sheaf of ring。

为什么要有sheaf这个概念呢？我觉得是为了研究每个点local的性质：一个点“附近”有多少种函数。所以就有了stalk的概念：一个点 x ∈ X，找到一个sequence of open sets：x ∈ ... U₃ ⊆ U₂ ⊆ U₁ ⊆ U₀=X。每一个开集都对应一个module of functions，然后求极限，这跟函数的极限也很像，就得到 sheaf stalk at x。

Sheaf就是为了研究stalk，意思是说sheaf之间的关系是从stalk来定义的。比如两个sheaf S₁ --> S₂，它的injection定义为在所有stalk上为injection。

可以搜一下sheaf of rings，group等等，随便添上一个结构的名字或者什么，都能搜到。这些结构不是函数，也未必是函子（functor）

[forecasting]

数学里另一个比较普遍的思想就是近似或者逼近，用相对简单的东西去近似或者逼近复杂的，比如用直线，平面等等去逼近或者拼接复杂的形体。
我自己觉得数学里的方法真的很少。创新主要基于metaphor（有一本书叫 Mathematics as Metaphor: Selected Essays of Yuri I. Manin），类比，归纳（不是数学归纳法），或者基于相关联的猜测。

至于形式化，比如弄范畴论或者数理逻辑，甚或证明，不过就是为了放心或者获取进一步的直觉，或者说得高大上一点，严格或找一些例子；没有那么重要，尤其形式化/抽象。代数几何的意大利学派像F.Enriques就曾经跟Zariski讲过这种话：“像我这样的贵族用不着去证明定理。证明由你们一介平民去做就行。”
不完全赞同恩里克斯的话，可在直觉和形式化之间寻求一个平衡还是必要的。

对了，没必要弄懂所有一方向的知识再去做研究，差不多就开始好了，缺啥，自己会补充。没看弃婴千枝子，理论物理好像无所不懂，可啥也没做出来 。

好了，狂人之言，诸位圣贤择焉

[TheMatrix]

对了，没必要弄懂所有一方向的知识再去做研究，差不多就开始好了，缺啥，自己会补充。没看弃婴千枝子，理论物理好像无所不懂，可啥也没做出来 。

当然。本版都是研究者。没有学生。

[TheMatrix]

为什么要有sheaf这个概念呢？我觉得是为了研究每个点local的性质：一个点“附近”有多少种函数。所以就有了stalk的概念：一个点 x ∈ X，找到一个sequence of open sets：x ∈ ... U₃ ⊆ U₂ ⊆ U₁ ⊆ U₀=X。每一个开集都对应一个module of functions，然后求极限，这跟函数的极限也很像，就得到 sheaf stalk at x。

Sheaf就是为了研究stalk，意思是说sheaf之间的关系是从stalk来定义的。比如两个sheaf S₁ --> S₂，它的injection定义为在所有stalk上为injection。

[FoxMe]

sheaf是解析函数的解析延拓概念的推广，它只能局部定义。代数几何的问题是概念太多。这里有几个概念：

sheaf, 束。把一些麦秆捆起来得到一束。
stalk, 秆。一束麦子的其中一根秆，很形象。
germ, 胚。胚芽发育成麦秆？两个函数局部相同，叫作同胚？

还有纤维从finer bundle,这里bundle也是捆，不知道和sheaf有关吗？

Sheaf就是functor。Sheaf是 contravariant functor on a topological space。一个空间X的拓扑可以看作是一个category T：object是开集，morphism是开集之间的inclusion关系。

Sheaf是T上的functor。但是它没说这个functor的target是哪。Target可以是module of functions，这是一个category。也就是每一个开集上的全部function，这是一个module。这种情况可以说sheaf of module，或者sheaf of function。Target还可以是group。还可以是ring。可以说Sheaf of group, sheaf of ring。

为什么要有sheaf这个概念呢？我觉得是为了研究每个点local的性质：一个点“附近”有多少种函数。所以就有了stalk的概念：一个点 x ∈ X，找到一个sequence of open sets：x ∈ ... U₃ ⊆ U₂ ⊆ U₁ ⊆ U₀=X。每一个开集都对应一个module of functions，然后求极限，这跟函数的极限也很像，就得到 sheaf stalk at x。

Sheaf就是为了研究stalk，意思是说sheaf之间的关系是从stalk来定义的。比如两个sheaf S₁ --> S₂，它的injection定义为在所有stalk上为injection。