Z_p一问
版主: verdelite, TheMatrix
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
#3 Re: Z_p一问
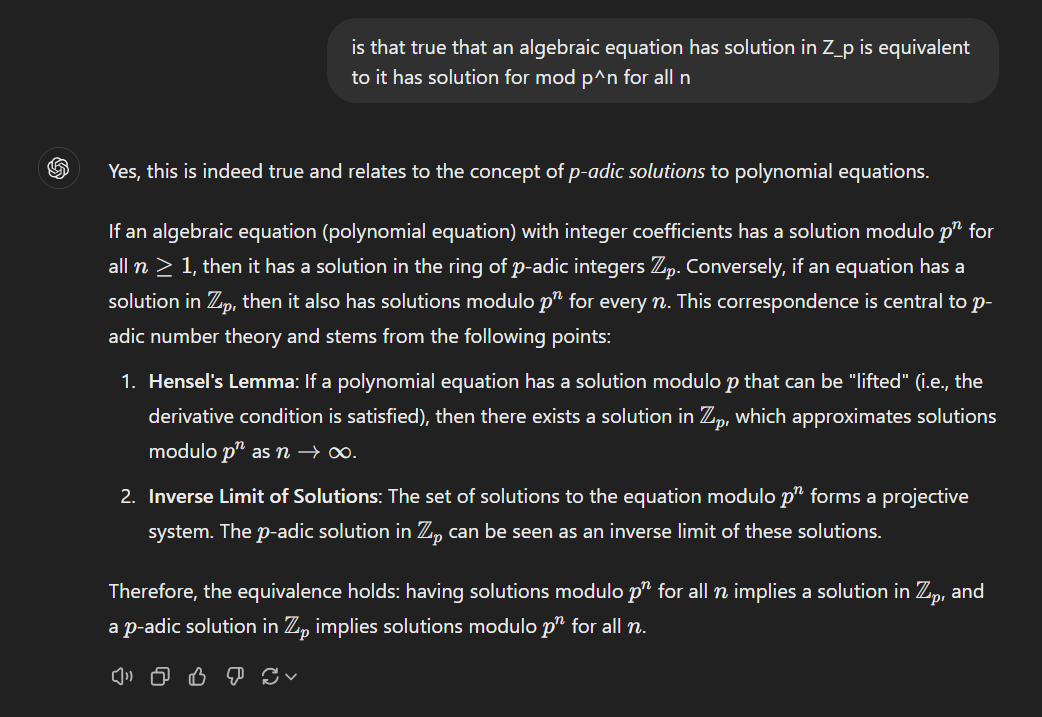
在Z7(7-adic integer)下有解怎么定义的?TheMatrix 写了: 2024年 11月 13日 20:14 给定素数p,比如p=7。一个代数方程,比如 x2+y2=5,如果mod 任意 7n有解,那么就在Z7(7-adic integer)下有解。这个对吧?
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
#5 Re: Z_p一问
Z7是一个ring。在一个ring下就可以定义一个代数方程。方程的解的定义也就清楚了。
一个ring R,考虑一个R系数二元polynomial p(x,y) ∈ R[x,y],一个代数方程就是 p(x,y)=0,解出 (x,y) ∈ R2 就是代数方程的解。
所以这个问题,以及我最初的问题,实际上是在问Z7是什么。为什么 x2+y2=5 是 Z7上的一个代数方程。也就是系数,包括常数,是否属于Z7。显然是属于的。所以一个代数方程在Z7下有解,这个问题已经“清楚”了。
除了我们还没有说Z7到底是什么。没说Z7到底是什么,说“显然属于”也显然是不合适的。
那么Z7到底是什么?
#6 Re: Z_p一问
应该是对的吧,就是Z7的定义
Z7 = {a0 + a1 7 + a2 72 + ...}
Z7 = {a0 + a1 7 + a2 72 + ...}
TheMatrix 写了: 2024年 11月 13日 20:14 给定素数p,比如p=7。一个代数方程,比如 x2+y2=5,如果mod 任意 7n有解,那么就在Z7(7-adic integer)下有解。这个对吧?
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
#7 Re: Z_p一问
还是从general的方面讲,如果有一个ring homomorphism Φ: R --> S,那么一个R上的代数方程自动也是一个S上的代数方程,而且R上有解,自动导出S上有解。因为比如说 f ∈ R[x,y],那么 f'=Φ(f) ∈ S[x,y],也就是把任意系数 c ∈ R 变成系数 Φ(c) ∈ S。如果代数方程 f=0 在R上有解,也就是 f(x,y) = 0。那么 (Φ(x),Φ(y)) 就是 f'=Φ(f) 在 S 上的解。TheMatrix 写了: 2024年 11月 14日 11:14 Z7是一个ring。在一个ring下就可以定义一个代数方程。方程的解的定义也就清楚了。
一个ring R,考虑一个R系数二元polynomial p(x,y) ∈ R[x,y],一个代数方程就是 p(x,y)=0,解出 (x,y) ∈ R2 就是代数方程的解。
所以这个问题,以及我最初的问题,实际上是在问Z7是什么。为什么 x2+y2=5 是 Z7上的一个代数方程。也就是系数,包括常数,是否属于Z7。显然是属于的。所以一个代数方程在Z7下有解,这个问题已经“清楚”了。
除了我们还没有说Z7到底是什么。没说Z7到底是什么,说“显然属于”也显然是不合适的。
那么Z7到底是什么?
比如 Z --> Z/7Z,这是一个(surjective) ring homomorphism,一个代数方程,比如 x2+y2=5,在Z上有定义,在 Z/7Z上就自动有定义。在Z上有解,在Z/7Z上就自动有解。
注意从general方面来讲,Φ: R --> S 只需要是一个ring homomorphism,可以surjective,也可以injective,也可以不surjective也不injective。
上次由 TheMatrix 在 2024年 11月 14日 11:31 修改。
原因: 未提供修改原因
原因: 未提供修改原因
#8 Re: Z_p一问
好,我也来问个问题:
如果一个代数方程在Zp上有解(对所有素数p),能否推出在Z上有解?
如果一个代数方程在Zp上有解(对所有素数p),能否推出在Z上有解?
TheMatrix 写了: 2024年 11月 14日 11:28 还是从general的方面讲,如果有一个ring homomorphism Φ: R --> S,那么一个R上的代数方程自动也是一个S上的代数方程,而且R上有解,自动导出S上有解。因为比如说 f ∈ R[x,y],那么 f'=Φ(f) ∈ S[x,y],也就是把任意系数 c ∈ R 变成系数 Φ(c) ∈ S。如果代数方程 f=0 在R上有解,也就是 f(x,y) = 0。那么 (Φ(x),Φ(y)) 就是 f'=Φ(f) 在 S 上的解。
比如 Z --> Z/7Z,这是一个(surjective) ring homomorphism,一个代数方程,比如 x2+y2=5,在Z上有定义,在 Z/7Z上就自动有定义。在Z上有解,在Z/7Z上就自动有解。
注意从general方面来讲,Φ: R --> S 只需要是一个ring homomorphism,可以surjective,也可以injective,也可以不surjective也不injective。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
#9 Re: Z_p一问
所以又回到Z7到底是什么的问题。TheMatrix 写了: 2024年 11月 14日 11:28 还是从general的方面讲,如果有一个ring homomorphism Φ: R --> S,那么一个R上的代数方程自动也是一个S上的代数方程,而且R上有解,自动导出S上有解。因为比如说 f ∈ R[x,y],那么 f'=Φ(f) ∈ S[x,y],也就是把任意系数 c ∈ R 变成系数 Φ(c) ∈ S。如果代数方程 f=0 在R上有解,也就是 f(x,y) = 0。那么 (Φ(x),Φ(y)) 就是 f'=Φ(f) 在 S 上的解。
比如 Z --> Z/7Z,这是一个(surjective) ring homomorphism,一个代数方程,比如 x2+y2=5,在Z上有定义,在 Z/7Z上就自动有定义。在Z上有解,在Z/7Z上就自动有解。
注意从general方面来讲,Φ: R --> S 只需要是一个ring homomorphism,可以surjective,也可以injective,也可以不surjective也不injective。
我喜欢这个定义:Z7 是 inverse limit of
... --> Z/73Z --> Z/72Z --> Z/7Z --> 0
其中每一个箭头都是 surjective ring homomorphism。
inverse limit构造一般是product,也就是 ...* Z/73Z * Z/72Z * Z/7Z。其元素为 (...,a3,a2,a1)。也就是每一个元素an ∈ 每一个 product component Z/7nZ。
但是还有箭头连接的要求。也就是 an --> an-1 必须是从 Z/7nZ --> Z/7n-1Z 这个surjective homomorphism来的。比如 a2 = 13 (mod 49),那么 a1必须等于 6 (mod 7)。
这就是 Z7。这是我喜欢的定义。
还有用7-base进制定义数的方法来表示Z7的。这个需要加上Z7拓扑,我有点怕怕。
上次由 TheMatrix 在 2024年 11月 14日 11:50 修改。
原因: 未提供修改原因
原因: 未提供修改原因
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
#11 Re: Z_p一问
我比较适应第二种定义,而对于direct limit, inverse limit有点心慌 
TheMatrix 写了: 2024年 11月 14日 11:47 所以又回到Z7到底是什么的问题。
我喜欢这个定义:Z7 是 inverse limit of
... --> Z/73Z --> Z/72Z --> Z/7Z --> 0
其中每一个箭头都是 surjective ring homomorphism。
inverse limit构造一般是product,也就是 ...* Z/73Z * Z/72Z * Z/7Z。其元素为 (...,a3,a2,a1)。也就是每一个元素an ∈ 每一个 product component Z/7nZ。
但是还有箭头连接的要求。也就是 an --> an-1 必须是从 Z/7nZ --> Z/7n-1Z 这个surjective homomorphism来的。比如 a2 = 13 (mod 49),那么 a1必须等于 6 (mod 7)。
这就是 Z7。这是我喜欢的定义。
还有用7-base进制定义数的方法来表示Z7的。这个需要加上Z7拓扑,我有点怕怕。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
#12 Re: Z_p一问
这是纯代数定义的。作为product,Z7的加法和乘法就是component-wise 的加法和乘法。TheMatrix 写了: 2024年 11月 14日 11:47 所以又回到Z7到底是什么的问题。
我喜欢这个定义:Z7 是 inverse limit of
... --> Z/73Z --> Z/72Z --> Z/7Z --> 0
其中每一个箭头都是 surjective ring homomorphism。
inverse limit构造一般是product,也就是 ...* Z/73Z * Z/72Z * Z/7Z。其元素为 (...,a3,a2,a1)。也就是每一个元素an ∈ 每一个 product component Z/7nZ。
但是还有箭头连接的要求。也就是 an --> an-1 必须是从 Z/7nZ --> Z/7n-1Z 这个surjective homomorphism来的。比如 a2 = 13 (mod 49),那么 a1必须等于 6 (mod 7)。
这就是 Z7。这是我喜欢的定义。
还有用7-base进制定义数的方法来表示Z7的。这个需要加上Z7拓扑,我有点怕怕。
从这个定义直接得出两点:
1,Z7 --> Z/7nZ 有 projection - surjective homomorphism。
2,Z --> Z7 有一个 ring homomorphism。Z --> Z/7nZ factor through Z7。
Z --> Z7 是一个injective homomorphism。直接看的话,一个整数,比如62,在Z7中就表示为 (6,13,62,62,62,...)。也就是 62 mod 7n。
也就是Z包含在Z7中。Z7比Z大。这有点反直觉。
所以一个over Z的代数方程,自动也是over Z7的代数方程。有整数解,就自动有Z7解。但是反之不然。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
#13 Re: Z_p一问
既然Z7是个product:TheMatrix 写了: 2024年 11月 14日 13:24 这是纯代数定义的。作为product,Z7的加法和乘法就是component-wise 的加法和乘法。
从这个定义直接得出两点:
1,Z7 --> Z/7nZ 有 projection - surjective homomorphism。
2,Z --> Z7 有一个 ring homomorphism。Z --> Z/7nZ factor through Z7。
Z --> Z7 是一个injective homomorphism。直接看的话,一个整数,比如62,在Z7中就表示为 (6,13,62,62,62,...)。也就是 62 mod 7n。
也就是Z包含在Z7中。Z7比Z大。这有点反直觉。
所以一个over Z的代数方程,自动也是over Z7的代数方程。有整数解,就自动有Z7解。但是反之不然。
Z7 = Z/7Z * Z/72Z * Z/73Z * ...
而且其加法和乘法就是简单的component-wise加法和乘法,我想说一个代数方程在Z7有解就等价于其在所有Z/7nZ上有解。
唯一的问题是缺少序列之间的箭头:
(a1 <-- a2 <-- a3 <-- ...)
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
#16 Re: Z_p一问
Z7是不可数的,当然比Z大。可以和[0, 1]之间的实数类比,都可以表示为7进制无穷序列。
但是有个问题:x2 - 2 = 0这个方程在Z7里有两个根, 能认为它们代表了正负根号2吗?
但是有个问题:x2 - 2 = 0这个方程在Z7里有两个根, 能认为它们代表了正负根号2吗?
TheMatrix 写了: 2024年 11月 14日 13:24 这是纯代数定义的。作为product,Z7的加法和乘法就是component-wise 的加法和乘法。
从这个定义直接得出两点:
1,Z7 --> Z/7nZ 有 projection - surjective homomorphism。
2,Z --> Z7 有一个 ring homomorphism。Z --> Z/7nZ factor through Z7。
Z --> Z7 是一个injective homomorphism。直接看的话,一个整数,比如62,在Z7中就表示为 (6,13,62,62,62,...)。也就是 62 mod 7n。
也就是Z包含在Z7中。Z7比Z大。这有点反直觉。
所以一个over Z的代数方程,自动也是over Z7的代数方程。有整数解,就自动有Z7解。但是反之不然。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
#19 Re: Z_p一问
我发现我不懂Hensel Lemma。这里应该要用到它。TheMatrix 写了: 2024年 11月 14日 15:48 既然Z7是个product:
Z7 = Z/7Z * Z/72Z * Z/73Z * ...
而且其加法和乘法就是简单的component-wise加法和乘法,我想说一个代数方程在Z7有解就等价于其在所有Z/7nZ上有解。
唯一的问题是缺少序列之间的箭头:
(a1 <-- a2 <-- a3 <-- ...)
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
#20 Re: Z_p一问
比如TheMatrix 写了: 2024年 11月 14日 15:48 既然Z7是个product:
Z7 = Z/7Z * Z/72Z * Z/73Z * ...
而且其加法和乘法就是简单的component-wise加法和乘法,我想说一个代数方程在Z7有解就等价于其在所有Z/7nZ上有解。
唯一的问题是缺少序列之间的箭头:
(a1 <-- a2 <-- a3 <-- ...)
a1是f=0 mod p的解,
a2是f=0 mod p2的解,
a3是f=0 mod p3的解,
那么箭头
a1 <-- a2 <-- a3
代表
a2=a1 mod p
a3=a2 mod p2
只有这样,这个序列 (a1 <-- a2 <-- a3 <-- ...) 才构成一个Zp的元素。
所以只说 f=0 mod pn 对任意n有解是不够的。解之间要满足箭头关系,才能推出在Zp上有解。
上次由 TheMatrix 在 2024年 11月 15日 10:32 修改。
原因: 未提供修改原因
原因: 未提供修改原因
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13638
- 注册时间: 2022年 7月 26日 00:35
#21 Re: Z_p一问
ring homomorphism Φ: R --> S 可以推出
1,代数方程 f=0 over R 可以看作代数方程 f=0 over S。
2,代数方程 f=0 over R 有解 (x,y),那么代数方程 f=0 over S 一定有解 (Φ(x),Φ(y))。
但是反过来不行,代数方程 f=0 over S 有解,不一定能推出代数方程 f=0 over R 有解。
反过来叫lift。也就是代数方程 f=0 over S 的解,什么情况下能lift到代数方程 f=0 over R 的解。
如果Φ不是surjective的话,如果over S的解不在Φ的image当中,那肯定不能lift回去。
所以简单情况:Φ是surjective ring homomorphism。
比如 Φ: Z/p2Z --> Z/pZ。这就是Hensel Lemma要考虑的问题。