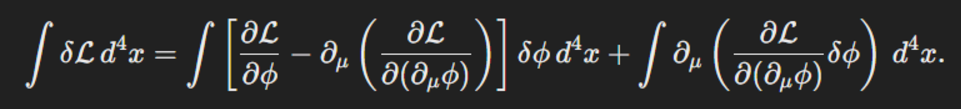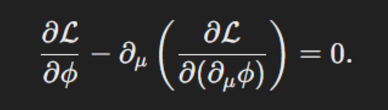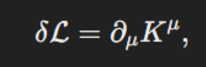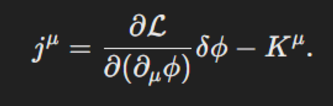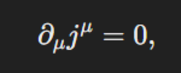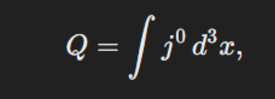连续对称性就是李群对称性(中的一个维度),也就是one parameter group。也就是在某一个变量的连续变化下,系统的方程不变,那么这个系统必然有一个相对应的不变量。
这就是我一直以来对Noether定理的理解。
这个理解应该说是对的。但是还缺少一些细节,以及一个常用的概念,就是conserved currents。这个概念是我一直没理解的。这几天看了一下。还是没有完全理解。
先问第一个问题:这里面出现的boundary term K是什么?
在下面这个图里。系列图在下一贴中。

版主: verdelite, TheMatrix




这段说的是同一个意思。但是对boundary term还是不太明白:TheMatrix 写了: 2024年 11月 30日 11:07 Noether定理是说,一个系统如果有一个连续对称性,那么它一定有一个相应的不变量。
连续对称性就是李群对称性(中的一个维度),也就是one parameter group。也就是在某一个变量的连续变化下,系统的方程不变,那么这个系统必然有一个相对应的不变量。
这就是我一直以来对Noether定理的理解。
这个理解应该说是对的。但是还缺少一些细节,以及一个常用的概念,就是conserved currents。这个概念是我一直没理解的。这几天看了一下。还是没有完全理解。
先问第一个问题:这里面出现的boundary term K是什么?
在下面这个图里。系列图在下一贴中。



哦。大概知道了。