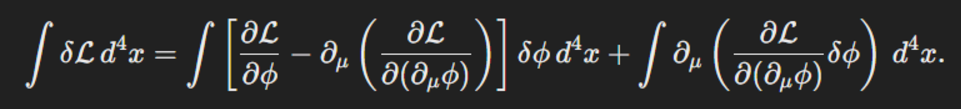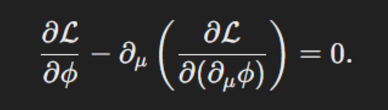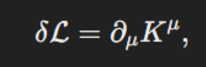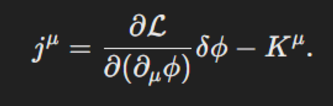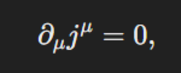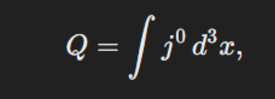新未名空间

Noether定理是说，一个系统如果有一个连续对称性，那么它一定有一个相应的不变量。

连续对称性就是李群对称性（中的一个维度），也就是one parameter group。也就是在某一个变量的连续变化下，系统的方程不变，那么这个系统必然有一个相对应的不变量。

这就是我一直以来对Noether定理的理解。

这个理解应该说是对的。但是还缺少一些细节，以及一个常用的概念，就是conserved currents。这个概念是我一直没理解的。这几天看了一下。还是没有完全理解。

先问第一个问题：这里面出现的boundary term K是什么？

在下面这个图里。系列图在下一贴中。

再追加一个解释为什么不出现 ∂L/∂ϕ 项：

TheMatrix 写了： 2024年 11月 30日 11:07 Noether定理是说，一个系统如果有一个连续对称性，那么它一定有一个相应的不变量。

连续对称性就是李群对称性（中的一个维度），也就是one parameter group。也就是在某一个变量的连续变化下，系统的方程不变，那么这个系统必然有一个相对应的不变量。

这就是我一直以来对Noether定理的理解。

这个理解应该说是对的。但是还缺少一些细节，以及一个常用的概念，就是conserved currents。这个概念是我一直没理解的。这几天看了一下。还是没有完全理解。

先问第一个问题：这里面出现的boundary term K是什么？

在下面这个图里。系列图在下一贴中。

这段说的是同一个意思。但是对boundary term还是不太明白：

TheMatrix 写了： 2024年 11月 30日 14:31 这段说的是同一个意思。但是对boundary term还是不太明白：

哦。大概知道了。

它的意思是，在对称性的一个方向上的变化，（通常是ϕ的一个变化），可以不使Lagrangian L本身不变，但是使action S=∫L不变。这也在Noether定理的范围内。

而L的变化，如果写成 L --> L+∂_μJ^μ，要使action不变，就必须
∫∂_μJ^μ = 0
体积分换成边界积分之后，相当于J^μ在边界积分等于0。如果J^μ在边界上本身就vanish，直接就满足这个条件了。

如果ϕ的变化直接导致Lagrangian L本身不变的话，那么这一项就没有了。

这里细节还真不少。

首先是变分法。变分法我没仔细研究过，但是依葫芦画瓢也能看懂：


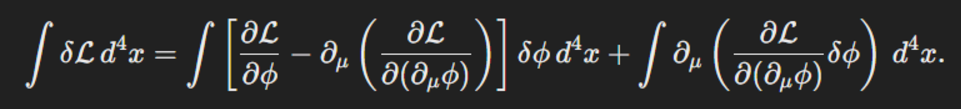
接下来这个正是Euler-Lagrange equation，也就是由L推出的运动方程。这个叫on-shell：


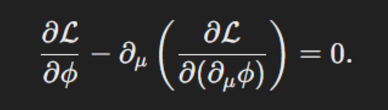
然后再把𝛿L表示成一个向量场的divergence。这是一个假设：


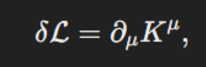
这样就得出一个conserved current j^μ：


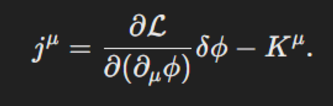
也就是divergence为0：


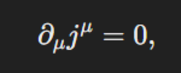
最后这一步也不容易：


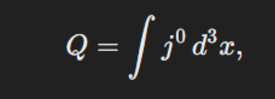
要展开写一下：

∂_μj^μ
= ∂_tj^t+∂_xj^x+∂_yj^y+∂_zj^z
= 0
其中j^t就是j⁰

所以
-∂_tj^t=∂_xj^x+∂_yj^y+∂_zj^z

注意这几个j^t,j^x,j^y,j^z,都是(t,x,y,z)的函数，求了偏导数之后还是(t,x,y,z)的函数。接下来只对(x,y,z)进行三元积分，积出来是t的函数：

∫∂_tj^t dxdydz = ∫∂_xj^x+∂_yj^y+∂_zj^z dxdydz

等式右边divergence积分换成boundary积分，这是高斯定理。因为对全空间积分，我们假设j这个向量在任意时间都是局域化的，也就是在空间(x,y,z)的无穷远处为0。所以等式右边等于0.

所以

d/dt ∫j^t dxdydz = ∫∂_tj^t dxdydz = 0

也就是 Q = ∫j^t dxdydz 是一个守恒量 - 对时间守恒。

TheMatrix 写了： 2024年 11月 30日 20:58
也就是divergence为0：


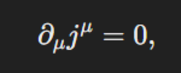
最后这一步也不容易：

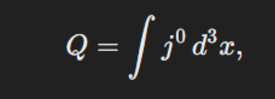
divergence等于0也叫incompressible。

incompressible，那么含量只和体积有关。固定一个体积，就有一个固定的含量。所以这里也有那个意思。不过这里不是对时间守恒。