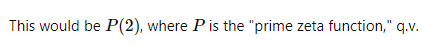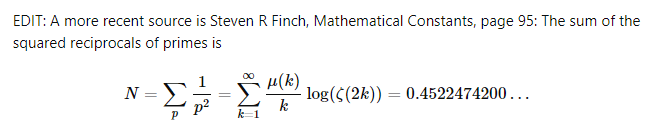因为素数在一个代数系统中是一个transcendental的存在。
一个代数系统 - 通常意义的代数系统 - 就是两种运算:加法和乘法。
就这么两种运算,就已经可以产生超难的问题:
x3+2x+1=0
y2=x3-x-3
难的问题都有一个特征:都是反问题。
即使是反问题,上面这些问题都有固定的幂次。
而素数没有固定的幂次 - 这是transcendental的特征。
来看看素数是怎么定义的:一个数是素数当它除了1和自己之外没有别的因子。
从这个定义可以看出,它是能够在一个代数系统中定义的。但是,它是以否定形式定义的。而以否定形式定义的物体,它就要求你一个一个检查过去。transcendental number是怎么定义的?不是代数数的,就是transcendental - 它也是否定形式定义的。在一个系统中以否定形式定义的概念,就是这个系统的超越概念。有点像集合和它的幂集的关系。
素数问题为什么难
版主: verdelite, TheMatrix
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13626
- 注册时间: 2022年 7月 26日 00:35
#2 Re: 素数问题为什么难
transcendental还和无穷有关。TheMatrix 写了: 2024年 1月 12日 09:57 因为素数在一个代数系统中是一个transcendental的存在。
一个代数系统 - 通常意义的代数系统 - 就是两种运算:加法和乘法。
就这么两种运算,就已经可以产生超难的问题:
x3+2x+1=0
y2=x3-x-3
难的问题都有一个特征:都是反问题。
即使是反问题,上面这些问题都有固定的幂次。
而素数没有固定的幂次 - 这是transcendental的特征。
来看看素数是怎么定义的:一个数是素数当它除了1和自己之外没有别的因子。
从这个定义可以看出,它是能够在一个代数系统中定义的。但是,它是以否定形式定义的。而以否定形式定义的物体,它就要求你一个一个检查过去。transcendental number是怎么定义的?不是代数数的,就是transcendental - 它也是否定形式定义的。在一个系统中以否定形式定义的概念,就是这个系统的超越概念。有点像集合和它的幂集的关系。
素数的检查步骤虽然为有限,但是没有上限。这话看着矛盾,但是我们都知道意思。
来看一个问题吧:任何4k+1的素数,必是某n2+1的因子。
写出来可以是:for any 4k+1 prime p, there exist m and n, such that mp-1=n2.
看着挺简单的。但是关键是:这个4k+1的prime p,无法描述进那个方程。必须用“话”来说。
#3 Re: 素数问题为什么难
数论的问题是离散问题,通常比连续问题难得多。
>就这么两种运算,就已经可以产生超难的问题:
我也有同感,群只有一种运算,环有两种。所以环有很多难题,而群论中的很多问题已经解决。
>就这么两种运算,就已经可以产生超难的问题:
我也有同感,群只有一种运算,环有两种。所以环有很多难题,而群论中的很多问题已经解决。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13626
- 注册时间: 2022年 7月 26日 00:35
#4 Re: 素数问题为什么难
嗯。代数结构中,还没有超过两种以上的运算层级。二元运算,就是加法和乘法。这是两层。FoxMe 写了: 2024年 1月 12日 12:51 数论的问题是离散问题,通常比连续问题难得多。
>就这么两种运算,就已经可以产生超难的问题:
我也有同感,群只有一种运算,环有两种。所以环有很多难题,而群论中的很多问题已经解决。
有很多代数结构可以有多于一个的乘法,但是层级还是两层。比如matrix algebra,乘法可以是普通matrix乘法AB,还可以是李代数那种乘法:[A,B]=AB-BA。但是层级还是两层 - 普通乘法和李代数的乘法在同一层级,都是在加法之上的。
好像没有三层的代数结构。
依照整数的模型,加法,乘法,接下来应该是指数。
#5 Re: 素数问题为什么难
因为素数集合是一个递归集或可计算集,而且应该是计算复杂性为NP或NP-Hard的集合。TheMatrix 写了: 2024年 1月 12日 09:57 因为素数在一个代数系统中是一个transcendental的存在。
一个代数系统 - 通常意义的代数系统 - 就是两种运算:加法和乘法。
就这么两种运算,就已经可以产生超难的问题:
x3+2x+1=0
y2=x3-x-3
难的问题都有一个特征:都是反问题。
即使是反问题,上面这些问题都有固定的幂次。
而素数没有固定的幂次 - 这是transcendental的特征。
来看看素数是怎么定义的:一个数是素数当它除了1和自己之外没有别的因子。
从这个定义可以看出,它是能够在一个代数系统中定义的。但是,它是以否定形式定义的。而以否定形式定义的物体,它就要求你一个一个检查过去。transcendental number是怎么定义的?不是代数数的,就是transcendental - 它也是否定形式定义的。在一个系统中以否定形式定义的概念,就是这个系统的超越概念。有点像集合和它的幂集的关系。
任何问题的证明难度和寻找证明的难度(元计算复杂性理论)都跟计算复杂性有关。奇怪的是停机问题,不完备定理等等的难度没那么高。
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13626
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 277
- 帖子: 13626
- 注册时间: 2022年 7月 26日 00:35