STEM版,合并数学,物理,化学,科学,工程,机械。不包括生物、医学相关,和计算机相关内容。
版主: verdelite, TheMatrix
-
(ヅ)楼主
- 论坛支柱

- 帖子互动: 549
- 帖子: 11819
- 注册时间: 2022年 8月 21日 14:20
帖子
由 (ヅ)楼主 »
根据上面那个勾股定理推广,猜想
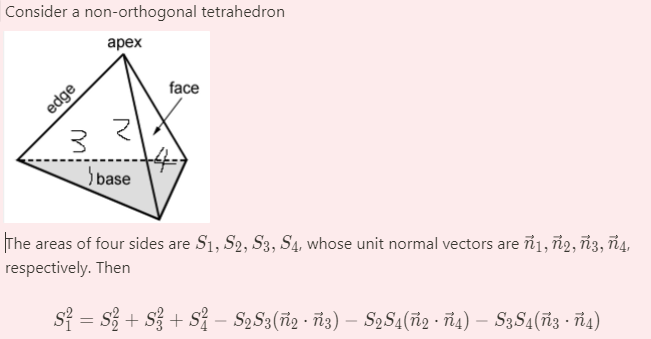
找了下,已经有人证明了
上次由 (ヅ) 在 2022年 12月 26日 13:11 修改。
-
TheMatrix
- 论坛支柱

2024年度优秀版主
TheMatrix 的博客
- 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix »
(ヅ) 写了: 2022年 12月 26日 13:03
根据上面那个勾股定理推广,猜想

找了下,已经有人证明了
能不能把
S
1,S
2,S
3,S
4,
n
1,n
2,n
3,n
4
写在同一边,搞一个轮换对称式?
-
YWY(夜未央)
- 论坛元老

2023-24年度十大优秀网友
- 帖子互动: 1332
- 帖子: 14369
- 注册时间: 2022年 7月 22日 17:25
帖子
由 YWY(夜未央) »
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
(ヅ)楼主
- 论坛支柱

- 帖子互动: 549
- 帖子: 11819
- 注册时间: 2022年 8月 21日 14:20
帖子
由 (ヅ)楼主 »
-
Caravel
- 论坛元老

Caravel 的博客
- 帖子互动: 676
- 帖子: 26902
- 注册时间: 2022年 7月 24日 17:21
帖子
由 Caravel »
TheMatrix 写了: 2022年 12月 26日 13:30
能不能把
S
1,S
2,S
3,S
4,
n
1,n
2,n
3,n
4
写在同一边,搞一个轮换对称式?
四个面积法向量之和等于0。然后内积一下?
-
TheMatrix
- 论坛支柱

2024年度优秀版主
TheMatrix 的博客
- 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix »
Caravel 写了: 2022年 12月 26日 14:15
四个面积法向量之和等于0。然后内积一下?
四个面积法向量之和一般不等于0,可变。
-
Caravel
- 论坛元老

Caravel 的博客
- 帖子互动: 676
- 帖子: 26902
- 注册时间: 2022年 7月 24日 17:21
帖子
由 Caravel »
TheMatrix 写了: 2022年 12月 26日 14:18
四个面积法向量之和一般不等于0,可变。
封闭曲面的面积法向量之和等于0,不成立么?二维是成立的吧
-
TheMatrix
- 论坛支柱

2024年度优秀版主
TheMatrix 的博客
- 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix »
Caravel 写了: 2022年 12月 26日 14:24
封闭曲面的面积法向量之和等于0,不成立么?二维是成立的吧
你想啊,三个面可以固定,另一个面滑动,所以法向量之和可变。
-
Caravel
- 论坛元老

Caravel 的博客
- 帖子互动: 676
- 帖子: 26902
- 注册时间: 2022年 7月 24日 17:21
帖子
由 Caravel »
TheMatrix 写了: 2022年 12月 26日 14:27
你想啊,三个面可以固定,另一个面滑动,所以法向量之和可变。
不是单位法向量,是带面积大小的。楼主那个公式不就是多项式定理么,这才是最一般的定理
-
TheMatrix
- 论坛支柱

2024年度优秀版主
TheMatrix 的博客
- 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix »
Caravel 写了: 2022年 12月 26日 14:32
不是单位法向量,是带面积大小的。
哦。那可能是对的。这个表达也是很简洁的。
-
TheMatrix
- 论坛支柱

2024年度优秀版主
TheMatrix 的博客
- 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix »
Caravel 写了: 2022年 12月 26日 14:32
不是单位法向量,是带面积大小的。楼主那个公式不就是多项式定理么,这才是最一般的定理
多项式定理?没看出来。
-
Caravel
- 论坛元老

Caravel 的博客
- 帖子互动: 676
- 帖子: 26902
- 注册时间: 2022年 7月 24日 17:21
帖子
由 Caravel »
TheMatrix 写了: 2022年 12月 26日 14:38
多项式定理?没看出来。
s1 + s2 + s3+ s4 平方和等于0,当然是向量形式的
-
TheMatrix
- 论坛支柱

2024年度优秀版主
TheMatrix 的博客
- 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
帖子
由 TheMatrix »
Caravel 写了: 2022年 12月 26日 15:05
s1 + s2 + s3+ s4 平方和等于0,当然是向量形式的
嗯对。平方和等于0。展开就能搞出不少东西。
-
YWY(夜未央)
- 论坛元老

2023-24年度十大优秀网友
- 帖子互动: 1332
- 帖子: 14369
- 注册时间: 2022年 7月 22日 17:25
帖子
由 YWY(夜未央) »
Caravel 写了: 2022年 12月 26日 14:32
不是单位法向量,是带面积大小的。楼主那个公式不就是多项式定理么,这才是最一般的定理
Caravel 写了: 2022年 12月 26日 15:05
s1 + s2 + s3+ s4 平方和等于0,当然是向量形式的
你这个思路很好,至少我是第一次知道。但用你的方法,也是用“加了(外指)法向量的s1 + s2 + s3+ s4 ”与自己做内积,然后通过这个内积是零,推导出余弦定理,推导过程也不是很显然吧。我用二维的三角形试推了一下,能推过去,但中间有推导,对我来说不显然。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
Caravel
- 论坛元老

Caravel 的博客
- 帖子互动: 676
- 帖子: 26902
- 注册时间: 2022年 7月 24日 17:21
帖子
由 Caravel »
YWY 写了: 2022年 12月 26日 15:21
你这个思路很好,至少我是第一次知道。但用你的方法,也是用“加了(外指)法向量的s1 + s2 + s3+ s4 ”与自己做内积,然后通过这个内积是零,推导出余弦定理,推导过程也不是很显然吧。我用二维的三角形试推了一下,能推过去,但中间有推导,对我来说不显然。
这个定理比余弦定理更强,而且可能可以推广到任意多面体,不需要是三角锥











