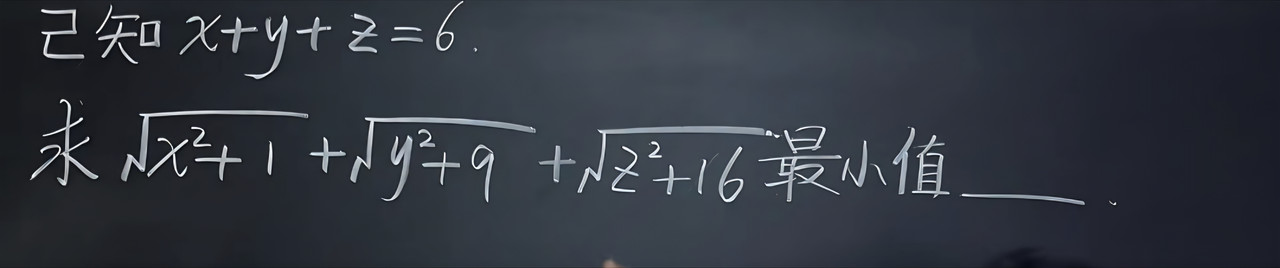这个太厉害了ILoveBainiu 写了: 2025年 6月 26日 23:14 The expression to minimize is sqrt(x² + 1²) + sqrt(y² + 3²) + sqrt(z² + 4²).
Each term in the sum can be interpreted as the length of the hypotenuse of a right triangle, or as the distance between two points in a 2D plane.
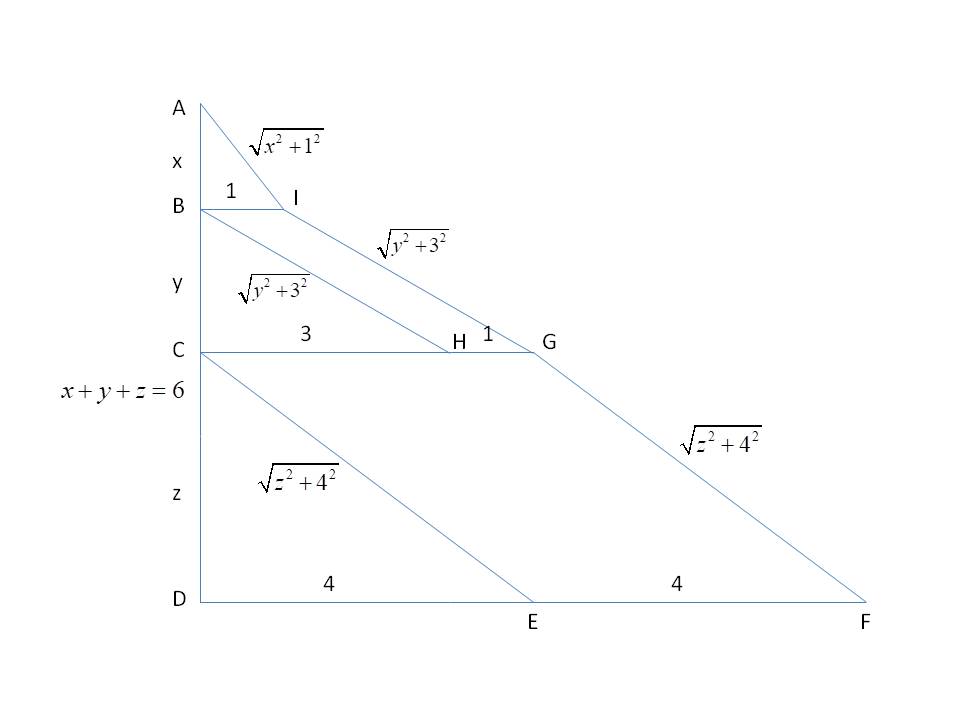
Let's visualize this as the length of a path made of three segments:
A segment with a horizontal displacement of x and a vertical displacement of 1. Its length is sqrt(x² + 1²).
A segment with a horizontal displacement of y and a vertical displacement of 3. Its length is sqrt(y² + 3²).
A segment with a horizontal displacement of z and a vertical displacement of 4. Its length is sqrt(z² + 4²).
The total length of this path is the sum we want to minimize. The path starts at an origin point, say (0,0), and ends at the point whose coordinates are the sum of the displacements.
The total horizontal displacement is x + y + z.
The total vertical displacement is 1 + 3 + 4 = 8.
We are given the constraint that x + y + z = 6. Therefore, the path connects the starting point (0, 0) to the fixed endpoint (6, 8).
The sum of the lengths of the path segments is minimized when the path is a straight line. The minimum value of the expression is therefore the straight-line distance between the point (0, 0) and the point (6, 8).
We can calculate this distance using the distance formula:
Distance = sqrt((6 - 0)² + (8 - 0)²)
Distance = sqrt(6² + 8²)
Distance = sqrt(36 + 64)
Distance = sqrt(100)
Distance = 10
Thus, the smallest possible value of the expression is 10.
看看gemini多牛逼
陈立人小时候做过的数学题,mit会做的不超过五个
版主: Softfist
-
juderiverman(兄弟是朱德)

- 著名点评

juderiverman 的博客 - 帖子互动: 247
- 帖子: 3495
- 注册时间: 2022年 9月 28日 08:36
#21 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
“We achieve inner peace when our schedule aligns with our values.”
#23 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
sqrt(x^2+1) + sqrt(y^2+9) + sqrt(z^2+16) >=sqrt(2x) + sqrt(6y)+sqrt(8z)
有题目对称性得到
3(sqrt(x^2+1) + sqrt(y^2+9) + sqrt(z^2+16) ) >= (sqrt(2)+sqrt(6)+sqrt(8)) (sqrt(x) + sqrt(y)+sqrt(z))
(sqrt(x) + sqrt(y)+sqrt(z))^2 =x+y+z + sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(y) sqrt(z) =6+ sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(x) sqrt(z)
由柯西不等式 (x+y+x)^2>=(sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(x) sqrt(z))^2
sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(x) sqrt(z)<=6
3倍的最小值 是(sqrt(2)+sqrt(6)+sqrt(8))*sqrt(12)
最小值是 (2sqrt(6) +6sqrt(2)+8sqrt(3))/3
有题目对称性得到
3(sqrt(x^2+1) + sqrt(y^2+9) + sqrt(z^2+16) ) >= (sqrt(2)+sqrt(6)+sqrt(8)) (sqrt(x) + sqrt(y)+sqrt(z))
(sqrt(x) + sqrt(y)+sqrt(z))^2 =x+y+z + sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(y) sqrt(z) =6+ sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(x) sqrt(z)
由柯西不等式 (x+y+x)^2>=(sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(x) sqrt(z))^2
sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(x) sqrt(z)<=6
3倍的最小值 是(sqrt(2)+sqrt(6)+sqrt(8))*sqrt(12)
最小值是 (2sqrt(6) +6sqrt(2)+8sqrt(3))/3
上次由 yuzhou 在 2025年 6月 27日 00:43 修改。
-
juderiverman(兄弟是朱德)

- 著名点评

juderiverman 的博客 - 帖子互动: 247
- 帖子: 3495
- 注册时间: 2022年 9月 28日 08:36
#24 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
如果这样的话,X应该最大,Y其次,Z最小;yuzhou 写了: 2025年 6月 26日 23:34 sqrt(x^2+1) + sqrt(y^2+9) + sqrt(z^2+16) >=sqrt(2x) + sqrt(6y)+sqrt(8z)
假定X,Y,Z都是正整数,那应该是3,2,1……
sqrt(10)+sqrt(13)+sqrt(17)=10.891
这组值不如1,2,3……
sqrt(2)+sqrt(13)+sqrt(25)=10.0198
类似长方形到正方形的变化,应该是Z>Y>X,因为16>9>1。
“We achieve inner peace when our schedule aligns with our values.”
#25 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
这样不行的,不等式右边只是给了左边的一个下界,但不一定是下确界。比如说你可以说三个平方根之和肯定大于等于0, 但0不一定是最小值。下确界才是最小值。你列出来的那个值,算出来是9.08,确实比10小,但永远都到不了这么小。
yuzhou 写了: 2025年 6月 26日 23:34 sqrt(x^2+1) + sqrt(y^2+9) + sqrt(z^2+16) >=sqrt(2x) + sqrt(6y)+sqrt(8z)
有题目对称性得到
3(sqrt(x^2+1) + sqrt(y^2+9) + sqrt(z^2+16) ) >= (sqrt(2)+sqrt(6)+sqrt(8)) (sqrt(x) + sqrt(y)+sqrt(z))
(sqrt(x) + sqrt(y)+sqrt(z))^2 =x+y+z + sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(y) sqrt(z) =6+ sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(x) sqrt(z)
由柯西不等式 (x+y+x)^2>=(sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(x) sqrt(z))^2
sqrt(x) sqrt(y)+ sqrt(y) sqrt(z)+ sqrt(x) sqrt(z)<=6
3倍的最小值 是(sqrt(2)+sqrt(6)+sqrt(8))*(sqrt(12))/3
最小值是 (2sqrt(6) +6sqrt(2)+8sqrt(3))/3
#27 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
看来你得到白牛指导了。用几何解决代数问题是另一个维度ILoveBainiu 写了: 2025年 6月 26日 23:14 The expression to minimize is sqrt(x² + 1²) + sqrt(y² + 3²) + sqrt(z² + 4²).
Each term in the sum can be interpreted as the length of the hypotenuse of a right triangle, or as the distance between two points in a 2D plane.
Let's visualize this as the length of a path made of three segments:
A segment with a horizontal displacement of x and a vertical displacement of 1. Its length is sqrt(x² + 1²).
A segment with a horizontal displacement of y and a vertical displacement of 3. Its length is sqrt(y² + 3²).
A segment with a horizontal displacement of z and a vertical displacement of 4. Its length is sqrt(z² + 4²).
The total length of this path is the sum we want to minimize. The path starts at an origin point, say (0,0), and ends at the point whose coordinates are the sum of the displacements.
The total horizontal displacement is x + y + z.
The total vertical displacement is 1 + 3 + 4 = 8.
We are given the constraint that x + y + z = 6. Therefore, the path connects the starting point (0, 0) to the fixed endpoint (6, 8).
The sum of the lengths of the path segments is minimized when the path is a straight line. The minimum value of the expression is therefore the straight-line distance between the point (0, 0) and the point (6, 8).
We can calculate this distance using the distance formula:
Distance = sqrt((6 - 0)² + (8 - 0)²)
Distance = sqrt(6² + 8²)
Distance = sqrt(36 + 64)
Distance = sqrt(100)
Distance = 10
Thus, the smallest possible value of the expression is 10.
看看gemini多牛逼
-
ILoveBainiu
- 职业作家

- 帖子互动: 30
- 帖子: 736
- 注册时间: 2022年 12月 24日 00:10
-
ILoveBainiu
- 职业作家

- 帖子互动: 30
- 帖子: 736
- 注册时间: 2022年 12月 24日 00:10
-
LiuQiangDong(qqq)
- 论坛支柱

- 帖子互动: 360
- 帖子: 10896
- 注册时间: 2022年 12月 30日 01:59
#34 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
A nice problem with nice solutions.
2023年12月,张雪峰在一个直播片段中表示“文科都是服务业,什么是服务业?总结称一个字就是‘舔’,就是‘爷, 我给你笑一个’”。这一言论引发网民争议。
#39 Re: 陈立人小时候做过的数学题,mit会做的不超过五个
什么思维扩展,扩展了还是格局太小。你看不到题目顶(底)层的逻辑。要让几个受线性约束的变量之和最小,这几个变量互相要成比例。这就是这个问题最底层的逻辑,根据三角形的相似性,口算都可以得出xyz的值