Computer algebra 来了
版主: verdelite, TheMatrix
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
-
Caravel
- 论坛元老

Caravel 的博客 - 帖子互动: 676
- 帖子: 26921
- 注册时间: 2022年 7月 24日 17:21
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
Re: Computer algebra 来了
以前我说过“群是很贫瘠的土壤”,我的意思是如果只研究群的话,只研究整齐的群的话,那它就是很贫瘠。比如说A5吧。A5很大的,有60个元素,但它是一个单群。
想象一下,在这个群中漫游的话,碰到的一个一个元素,各不相同,但是仅仅是一个单群中的不同元素而已,除此之外说不出什么来了,所以说也可以说它们没什么不同 - 芸芸众生而已。
但是如果下到子集的层面,结构突然丰富起来了,因为子集它不是群,以群的办法研究不了,必须提出新的概念。
就好像在虚数 i 提出来之前,人们已经发现了一些二次方程的规律,在实数内就可以说,但是很复杂。复数的概念一出来,一切都简化了。
想象一下,在这个群中漫游的话,碰到的一个一个元素,各不相同,但是仅仅是一个单群中的不同元素而已,除此之外说不出什么来了,所以说也可以说它们没什么不同 - 芸芸众生而已。
但是如果下到子集的层面,结构突然丰富起来了,因为子集它不是群,以群的办法研究不了,必须提出新的概念。
就好像在虚数 i 提出来之前,人们已经发现了一些二次方程的规律,在实数内就可以说,但是很复杂。复数的概念一出来,一切都简化了。
Re: Computer algebra 来了
There are only 3 conjugacy classes in A_5, one containing identity (only), one containing (1 2)(3 4), while the other containing (1 2 3). Here we write a permutation as a product of disjoint cycles.TheMatrix 写了: 2022年 12月 24日 18:18 再来看一下A5的conjugacy class的划分。A5共有60个元素。分成5个共轭类:
有两个12个的,1个15个的,1个20个的,再加单位元:
The conjugacy class containing (1 2) and the class containing (1 2 3)(4 5) all consist of odd permutations. So yes, there are altogether 5 conjugacy classes in S_5.
For some silly reason, I missed the conjugacy class of (1 2 3 4), which is odd, and the class of (1 2 3 4 5), which is even. So, in S_5, there are 7 conjugacy classes, of which 4 classes are even.
上次由 YWY 在 2022年 12月 25日 19:47 修改。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
Re: Computer algebra 来了
我检查一下。YWY 写了: 2022年 12月 24日 21:07 There are only 3 conjugacy classes in A_5, one containing identity (only), one containing (1 2)(3 4), while the other containing (1 2 3). Here we write a permutation as a product of disjoint cycles.
The conjugacy class containing (1 2) and the class containing (1 2 3) all consist of odd permutations. So yes, there are altogether 5 conjugacy classes in S_5.
你的(1 2)(3 4) 的conjugacy class有几个元素?我的是15个。
你的(1 2 3)的conjugacy class 有几个元素?我的是20个。
S_5我算的是7个conjugacy class:
1 (0, 1, 2, 3, 4)
10 (0, 1, 2, 4, 3)
20 (0, 1, 3, 4, 2)
15 (0, 2, 1, 4, 3)
30 (0, 2, 3, 4, 1)
20 (1, 0, 3, 4, 2)
24 (1, 2, 3, 4, 0)
不过我的记法跟你的不一样,我就是记permutation,而且是从0开始。
(1 2)(3 4) 我记为 (1, 0, 3, 2, 4)
(1 2 3)我记为 (1, 2, 0, 3, 4)
Re: Computer algebra 来了
You are correct. I forgot the class of (1 2 3 4 5), which is even, and the class of (1 2 3 4), which is odd. So there are 7 conjugacy classes in S_5, with 4 of them in A_5.TheMatrix 写了: 2022年 12月 24日 21:26 我检查一下。
你的(1 2)(3 4) 的conjugacy class有几个元素?我的是15个。
你的(1 2 3)的conjugacy class 有几个元素?我的是20个。
S_5我算的是7个conjugacy class:
1 (0, 1, 2, 3, 4)
10 (0, 1, 2, 4, 3)
20 (0, 1, 3, 4, 2)
15 (0, 2, 1, 4, 3)
30 (0, 2, 3, 4, 1)
20 (1, 0, 3, 4, 2)
24 (1, 2, 3, 4, 0)
不过我的记法跟你的不一样,我就是记permutation,而且是从0开始。
(1 2)(3 4) 我记为 (1, 0, 3, 2, 4)
(1 2 3)我记为 (1, 2, 0, 3, 4)
上次由 YWY 在 2022年 12月 24日 21:38 修改。
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
Re: Computer algebra 来了
嗯。我也查到了。有一个wiki专门讲有限群的:YWY 写了: 2022年 12月 24日 21:31 I forgot the class of (1 2 3 4 5), which is even, and the class of (1 2 3 4), which is odd. So there are 7 conjugacy classes in S_5, with 4 of them in A_5.
https://groupprops.subwiki.org/wiki/Ele ... g_group:A5
你用什么算的?也是程序吧?
Re: Computer algebra 来了
我就是手算的,用到的技巧是:用product of disjoint cycles的方法算共轭运算非常简洁,也非常容易判断谁和谁共轭或不共轭;比如,(1 2 3) and (2 5 4) must belong to the same conjugacy class, because they are both 3 cycles. Similarly, (1 2)(3 4) and (2 5)(3 4) must belong to the same conjugacy class.TheMatrix 写了: 2022年 12月 24日 21:36 嗯。我也查到了。有一个wiki专门讲有限群的:
https://groupprops.subwiki.org/wiki/Ele ... g_group:A5
你用什么算的?也是程序吧?
持仓抄底锁利,你钱你定
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
看牛观猪喊熊,自娱自乐
股市变幻莫测,不作不死
赌途曲折无常,吃枣药丸
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
Re: Computer algebra 来了
cycle的方法我一直没有完全搞清楚。YWY 写了: 2022年 12月 24日 21:43 我就是手算的,用到的技巧是:用product of disjoint cycles的方法算共轭运算非常简洁,也非常容易判断谁和谁共轭或不共轭;比如,(1 2 3) and (2 5 4) must belong to the same conjugacy class, because they are both 3 cycles. Similarly, (1 2)(3 4) and (2 5)(3 4) must belong to the same conjugacy class.
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
-
mitbbsnew
- 论坛元老

mitbbsnew 的博客 - 帖子互动: 271
- 帖子: 18003
- 注册时间: 2022年 7月 22日 13:15
-
TheMatrix楼主

- 论坛支柱

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 271
- 帖子: 13563
- 注册时间: 2022年 7月 26日 00:35
Re: Computer algebra 来了
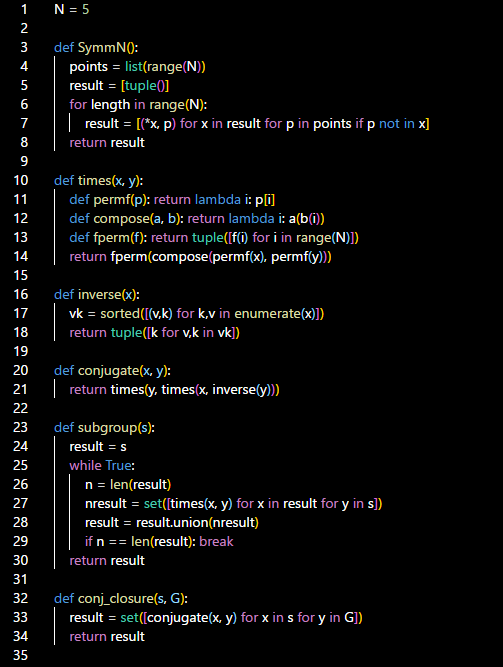
这里用了点symmetric group的知识。Symmetric group就是permutation (function)on N objects。写出来就是
(0,1,2,3,4) - 单位元
(3,2,0,1,4) - 看成函数的话就是 (0->3, 1->2, 2->0, 3->1, 4->4)
这样的。共有N!个。可以相乘 - 就是函数的合成, 构成了群。
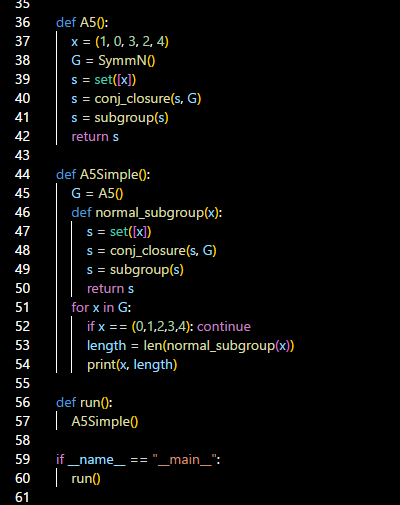
第一个函数 SymmN,就是写出N个元素的全部permutation。这个小问题放在LeetCode上,肯定不是easy的,至少是medium的。
第二个函数 times,就是permutation的乘法,也就是函数的合成。这在LeetCode上应该也是medium的。
第三个函数 inverse,就是一个permutation的inverse。这也得是medium的。
第四个函数conjugate,就是乘法 hgh-1。用乘法函数就简单了。
第五个函数 subgroup,是一个permutation的集合生成的子群,也就是以集合中元素各种乘法张成的子群。这个在LeetCode里应该是hard。
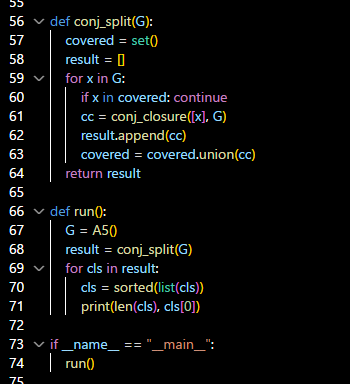
最后一个函数 conj_closure,是一个子集在全集中的全部conjugate。
Re: Computer algebra 来了
对。当初学群论的时候,同学们普遍的感觉是并不难,基本是中学排列组合的难度。YWY 写了: 2022年 12月 24日 21:43 我就是手算的,用到的技巧是:用product of disjoint cycles的方法算共轭运算非常简洁,也非常容易判断谁和谁共轭或不共轭;比如,(1 2 3) and (2 5 4) must belong to the same conjugacy class, because they are both 3 cycles. Similarly, (1 2)(3 4) and (2 5)(3 4) must belong to the same conjugacy class.