圆锥曲线与齐次方程
-
TheMatrix楼主

- 论坛元老

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 293
- 帖子: 13910
- 注册时间: 2022年 7月 26日 00:35
圆锥曲线与齐次方程
高中都学圆锥曲线。为什么学圆锥曲线不学圆柱曲线?就是因为圆锥曲线是齐次方程截取的曲线。圆锥曲面就是齐次方程的解集。而圆柱曲面不是。圆锥曲面和圆柱曲面都是直纹面 - 由一根一根直线组成的。但是圆锥曲面的每根直线都通过原点,不仅是直线,还是线性子空间。而圆柱曲面每根直线不是线性子空间。所以圆锥曲面圆锥曲线比较好研究。
不过圆锥曲面是二次曲面,圆锥曲线是二次曲线。扩展到三次就到了三次曲面和椭圆曲线。
圆锥曲线的方法,是先维度升上去,(升一维),然后在高一维的空间中,考察一个几何物体,以这个物体的不同截面,来统一低一维上的各种曲线。统一与联系,这是数学中的一个主题。
齐次方程还有一个好处,就是方便处理无穷大。拓扑上看,它是一个compact space。一个space它是compact的,就可以有穷尽分类研究的可能。
不过圆锥曲面是二次曲面,圆锥曲线是二次曲线。扩展到三次就到了三次曲面和椭圆曲线。
圆锥曲线的方法,是先维度升上去,(升一维),然后在高一维的空间中,考察一个几何物体,以这个物体的不同截面,来统一低一维上的各种曲线。统一与联系,这是数学中的一个主题。
齐次方程还有一个好处,就是方便处理无穷大。拓扑上看,它是一个compact space。一个space它是compact的,就可以有穷尽分类研究的可能。
-
TheMatrix楼主

- 论坛元老

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 293
- 帖子: 13910
- 注册时间: 2022年 7月 26日 00:35
Re: 圆锥曲线与齐次方程
我们研究的是曲线。这是一个一维的几何物体。但是它的方程,是二元函数表达的:f(x,y)=0。而要研究各个曲线之间的关系,还得把它们再升一维,变成圆锥曲面(上的截面)。也就是说要研究一维的曲线,我们升到了三维。
维度这个东西真是厉害,等级森严。低一维看高一维,无穷复杂。而高一维看低一维,一切都是明摆着的。这就叫降维打击。
维度这个东西真是厉害,等级森严。低一维看高一维,无穷复杂。而高一维看低一维,一切都是明摆着的。这就叫降维打击。
Re: 圆锥曲线与齐次方程
TheMatrix 写了: 2023年 2月 19日 13:31 高中都学圆锥曲线。为什么学圆锥曲线不学圆柱曲线?就是因为圆锥曲线是齐次方程截取的曲线。圆锥曲面就是齐次方程的解集。而圆柱曲面不是。圆锥曲面和圆柱曲面都是直纹面 - 由一根一根直线组成的。但是圆锥曲面的每根直线都通过原点,不仅是直线,还是线性子空间。而圆柱曲面每根直线不是线性子空间。所以圆锥曲面圆锥曲线比较好研究。
不过圆锥曲面是二次曲面,圆锥曲线是二次曲线。扩展到三次就到了三次曲面和椭圆曲线。
圆锥曲线的方法,是先维度升上去,(升一维),然后在高一维的空间中,考察一个几何物体,以这个物体的不同截面,来统一低一维上的各种曲线。统一与联系,这是数学中的一个主题。
齐次方程还有一个好处,就是方便处理无穷大。拓扑上看,它是一个compact space。一个space它是compact的,就可以有穷尽分类研究的可能。
圆柱是特殊的圆锥,反之则不然
-
TheMatrix楼主

- 论坛元老

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 293
- 帖子: 13910
- 注册时间: 2022年 7月 26日 00:35
-
meiyoumajia(没有马甲)
- 论坛元老

- 帖子互动: 56
- 帖子: 17352
- 注册时间: 2022年 7月 22日 15:16
- 来自: 宇宙
-
TheMatrix楼主

- 论坛元老

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 293
- 帖子: 13910
- 注册时间: 2022年 7月 26日 00:35
Re: 圆锥曲线与齐次方程
我是最近在研究,把一般的三次代数方程,变为标准椭圆曲线方程的时候,学习了齐次方程的方法。我也没有完全搞明白。
一般的三次代数方程(二元)有10项:
x3
y3
x2y
xy2
x2
y2
xy
x
y
1
可以变成标准椭圆曲线的形式:
y2=x3+px+q
首先把原方程齐次化,加个z。再用一个齐次线性变换,也就是换元法:
x -> a1x+b1+c1z
y -> a2x+b2+c2z
z -> a3x+b3+c3z
再代入z=1。这样就应该可以把原方程变成标准椭圆曲线的形式。也就是要找一个线性变换。
但是这是我觉得。不一定对。网上看了一些资料。确实有方法可以变成标准椭圆曲线。但是中间好像有一步不是线性变换。
-
TheMatrix楼主

- 论坛元老

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 293
- 帖子: 13910
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛元老

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 293
- 帖子: 13910
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛元老

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 293
- 帖子: 13910
- 注册时间: 2022年 7月 26日 00:35
Re: 圆锥曲线与齐次方程
空间想象真的很难。我现在知道3d打印有用了 - 把圆锥面打印出来,圆锥曲线就容易想象了。作3维图都不行,因为我们3维作图一般指的是电脑上用透视法做的图。它实际上还是2维的。而且透视法作图也很难。最关键的是shading。
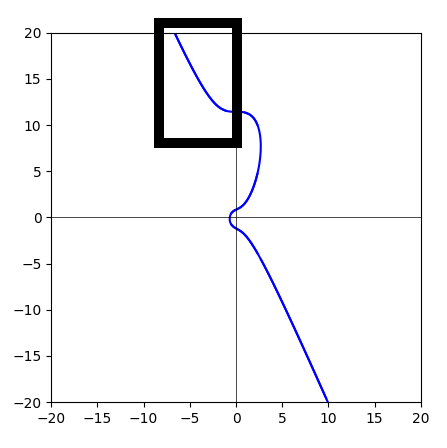
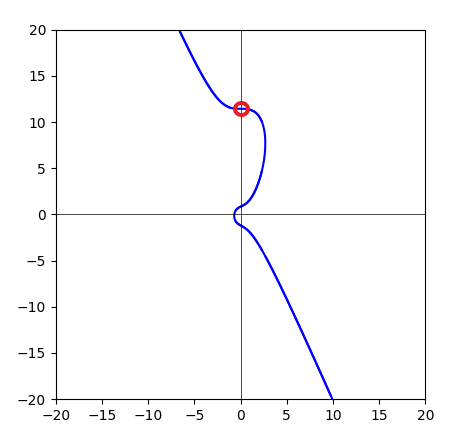
下面这张图是椭圆曲线:
y2 = x3+x+1
它对应的齐次方程是:
y2z = x3+xz2+z3
齐次方程的解,是一个直纹面。每一条直线都通过原点。而该曲线可以看成是这个直纹面被z=1平面截取出来的曲线。也可以说是广义的圆锥曲线。
现在给大家5分钟,脑袋里面想象一下这个直纹面。。。。
现在想象该直纹面以x-轴为旋转轴开始旋转 - 上半部分朝着我们的方向旋转。转到每一个角度的时候,仍然用z=1这个平面截取圆锥曲线。那么在每个旋转角度上截取出的圆锥曲线应该是什么样子?比如说,转动45°是什么样子?转动90°是什么样子?
下面这张图是椭圆曲线:
y2 = x3+x+1
它对应的齐次方程是:
y2z = x3+xz2+z3
齐次方程的解,是一个直纹面。每一条直线都通过原点。而该曲线可以看成是这个直纹面被z=1平面截取出来的曲线。也可以说是广义的圆锥曲线。

现在给大家5分钟,脑袋里面想象一下这个直纹面。。。。
现在想象该直纹面以x-轴为旋转轴开始旋转 - 上半部分朝着我们的方向旋转。转到每一个角度的时候,仍然用z=1这个平面截取圆锥曲线。那么在每个旋转角度上截取出的圆锥曲线应该是什么样子?比如说,转动45°是什么样子?转动90°是什么样子?
-
TheMatrix楼主

- 论坛元老

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 293
- 帖子: 13910
- 注册时间: 2022年 7月 26日 00:35
Re: 圆锥曲线与齐次方程
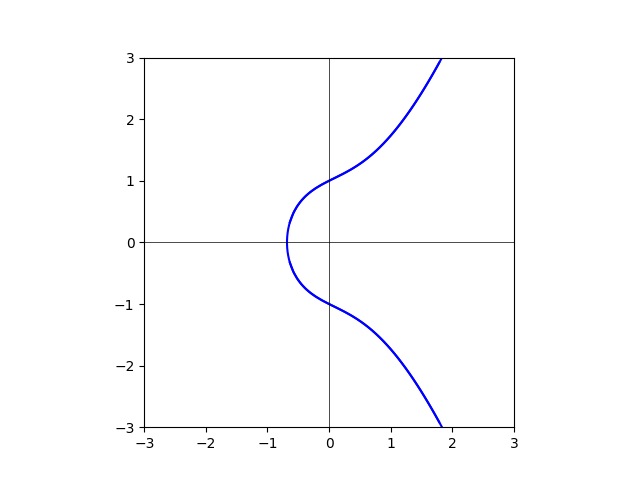
图我已经做出来了。但是还是不能在脑袋里把它的变化“形成”。放在这里,大家一起想。
degree=0

degree=5
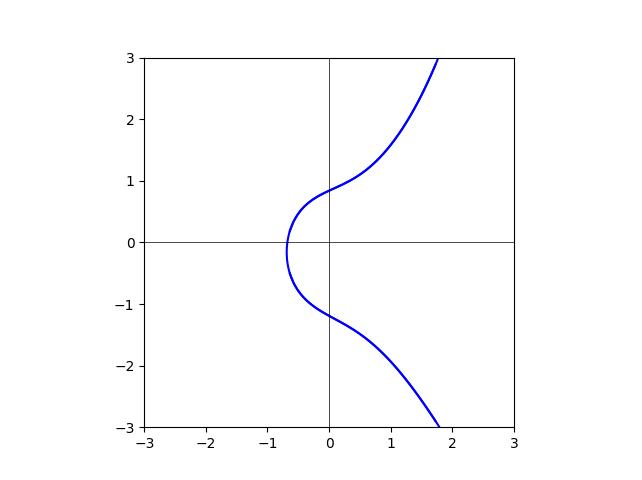
degree=10
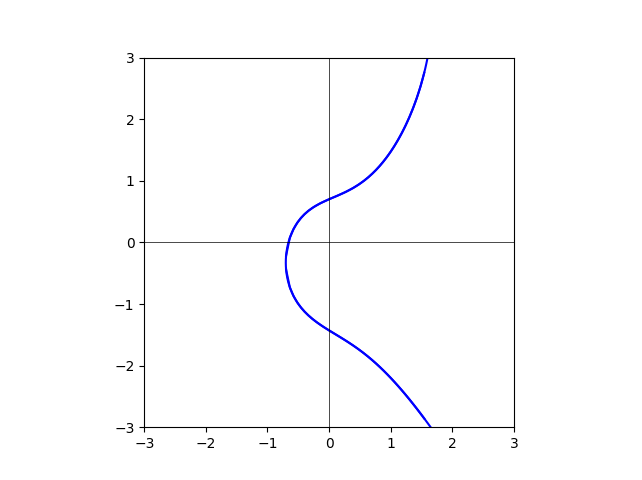
degree=15
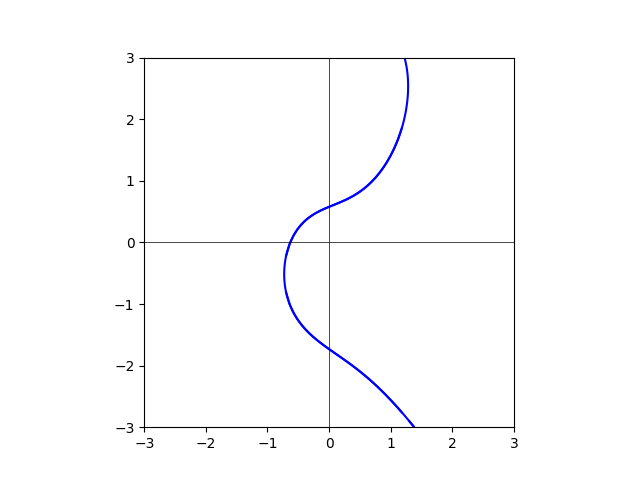
degree=20
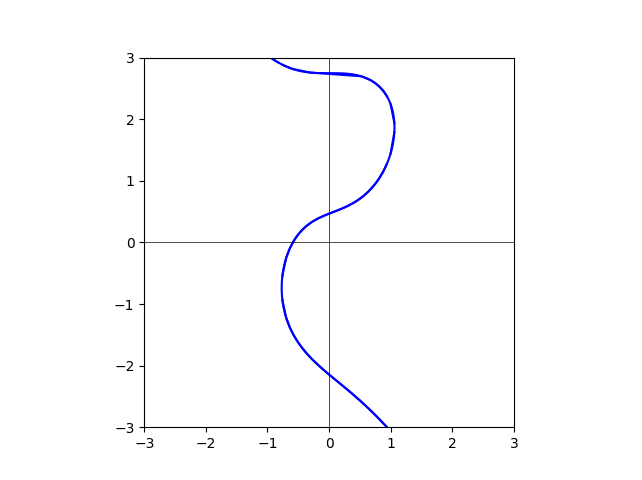
degree=25
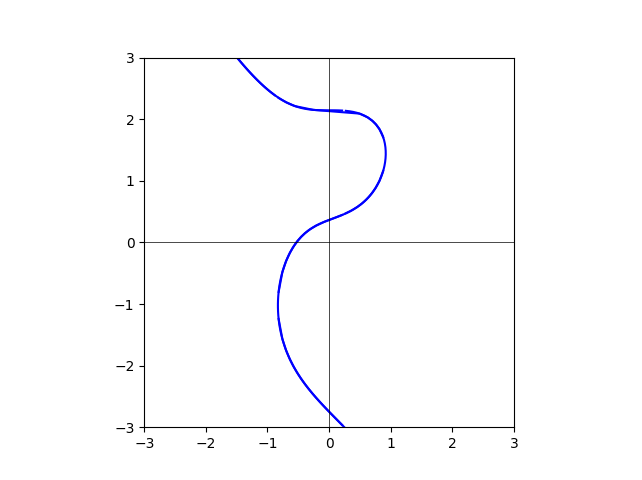
degree=30
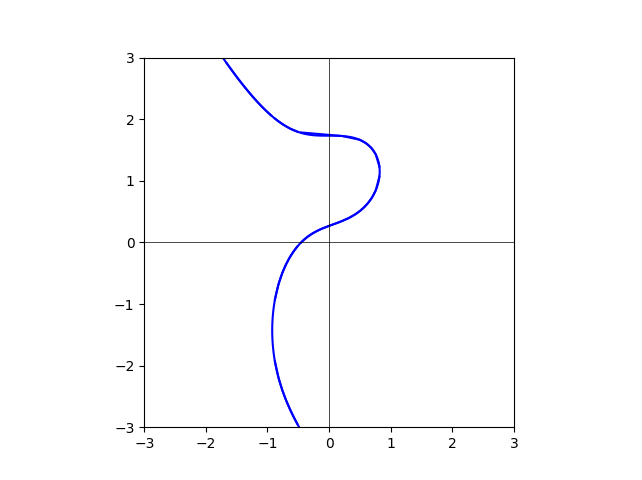
degree=35
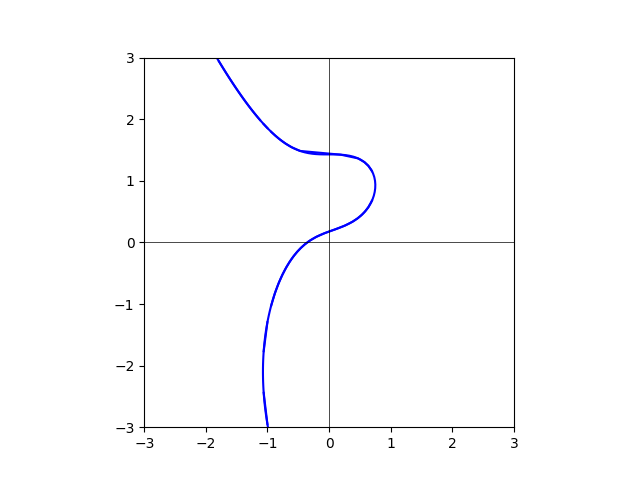
degree=40
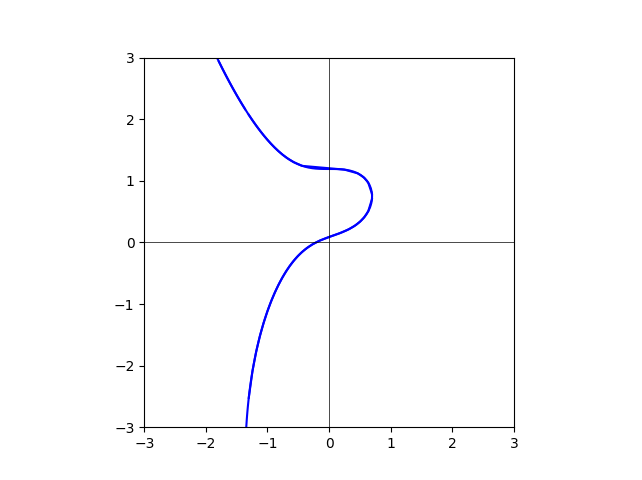
degree=45
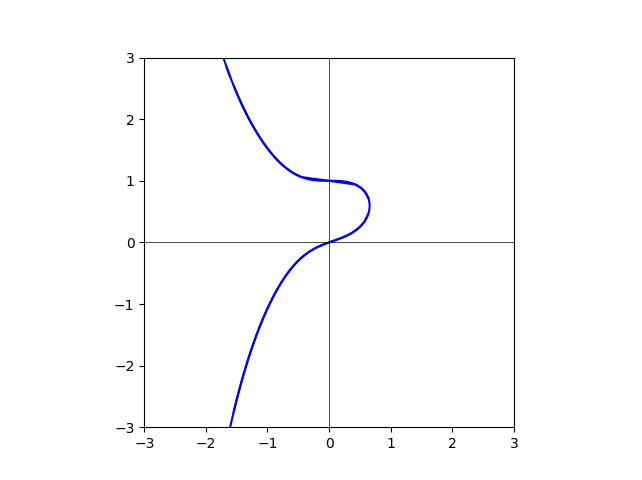
degree=50
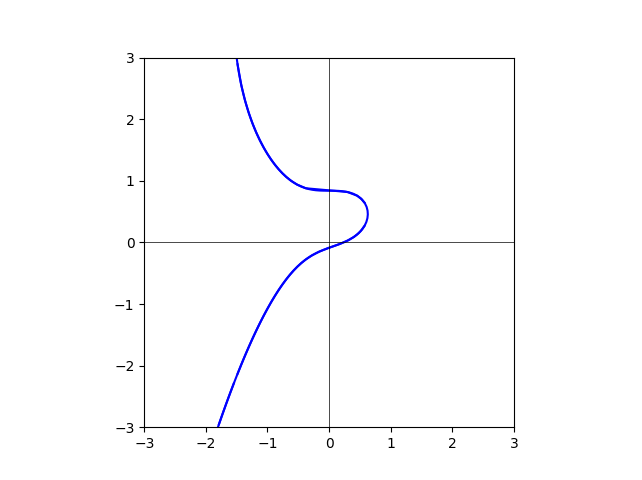
degree=55
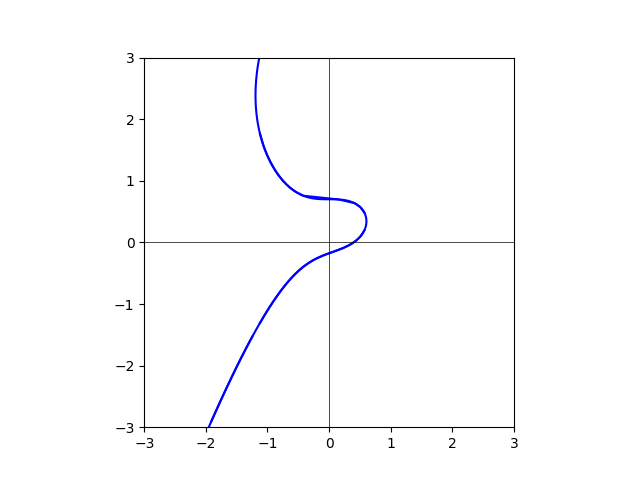
degree=60
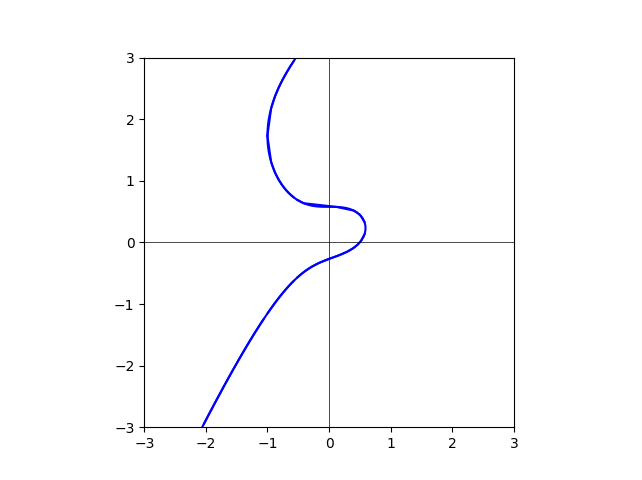
degree=65
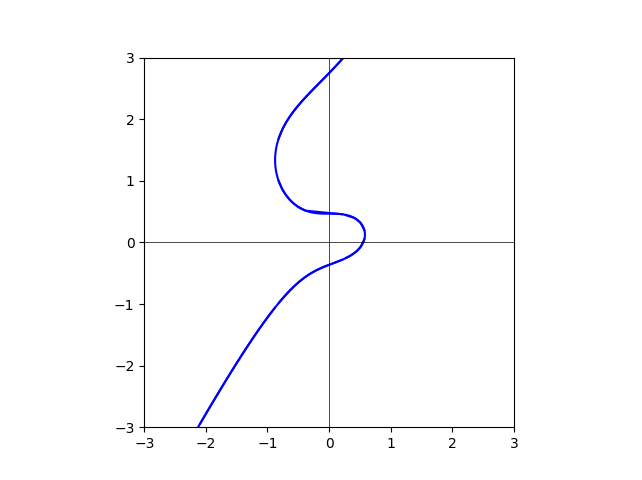
degree=70
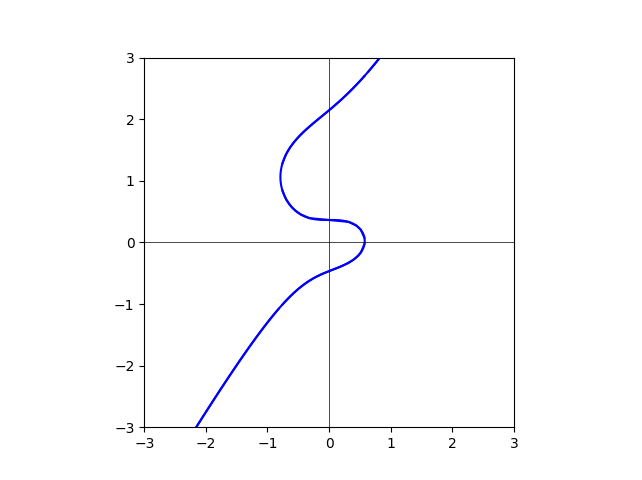
degree=75
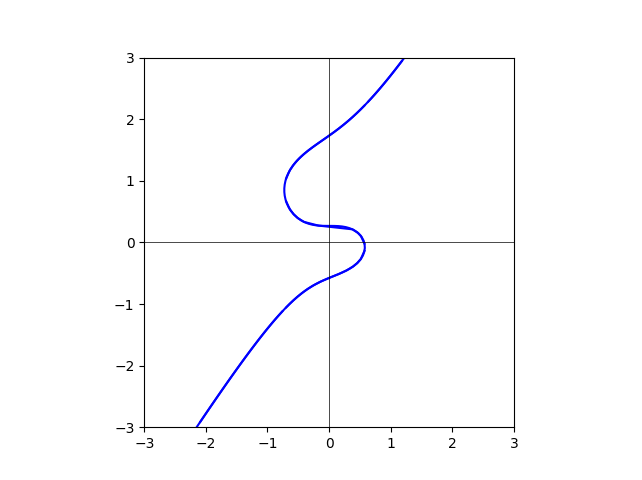
degree=80
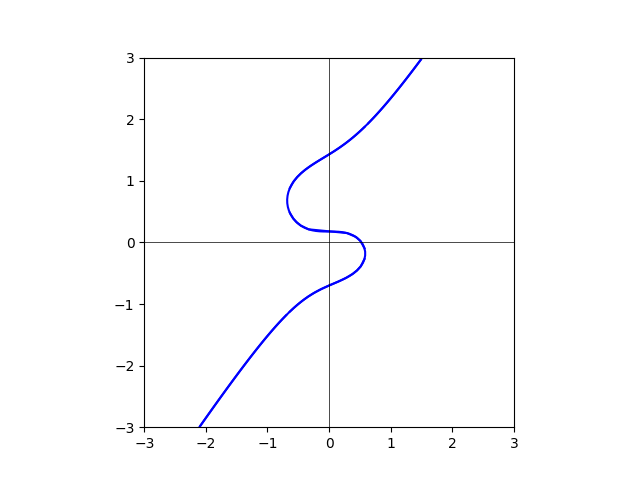
degree=85
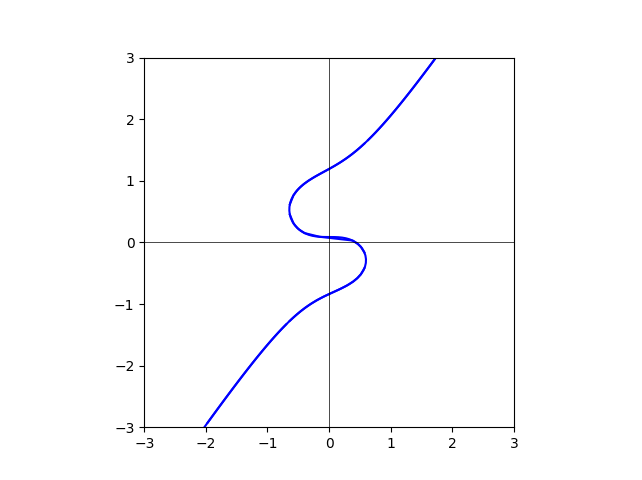
degree=90
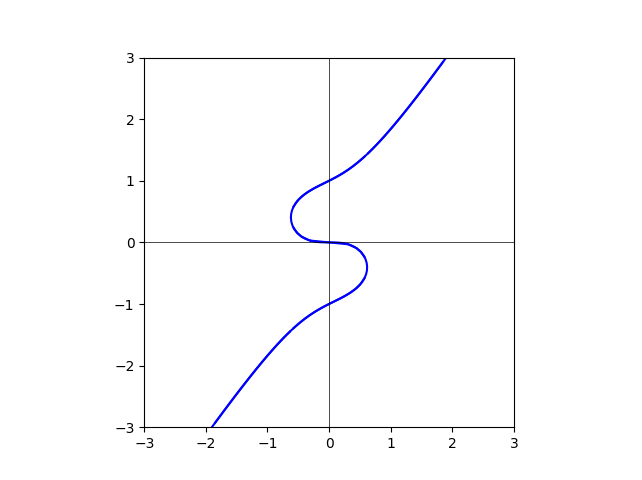
degree=0

degree=5

degree=10

degree=15

degree=20

degree=25

degree=30

degree=35

degree=40

degree=45

degree=50

degree=55

degree=60

degree=65

degree=70

degree=75

degree=80

degree=85

degree=90

-
TheMatrix楼主

- 论坛元老

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 293
- 帖子: 13910
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛元老

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 293
- 帖子: 13910
- 注册时间: 2022年 7月 26日 00:35
-
TheMatrix楼主

- 论坛元老

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 293
- 帖子: 13910
- 注册时间: 2022年 7月 26日 00:35
Re: 圆锥曲线与齐次方程
-
TheMatrix楼主

- 论坛元老

2024年度优秀版主
TheMatrix 的博客 - 帖子互动: 293
- 帖子: 13910
- 注册时间: 2022年 7月 26日 00:35